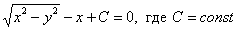Рассмотрим алгоритм решения уравнения в полных дифференциалах
Итак, требуется решить дифференциальное уравнение:
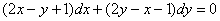
Действие первое. Пожалуйста, забудьте задачку про частные производные и готовый ответ. Дело в том, что когда вам предложен для решения произвольный диффур, то вы ещё не знаете о том, что это уравнение в полных дифференциалах. И данный факт крайне желательно доказать в самом начале решения.
Докажем, что уравнение 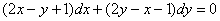 является уравнением в полных дифференциалах. Как это сделать? Уравнение в полных дифференциалах имеет вид
является уравнением в полных дифференциалах. Как это сделать? Уравнение в полных дифференциалах имеет вид 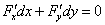 . Вспоминаем характерное и очень удобное равенство смешанных производных второго порядка:
. Вспоминаем характерное и очень удобное равенство смешанных производных второго порядка: 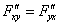 . Вот его и надо проверить:
. Вот его и надо проверить:
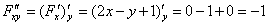
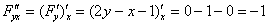
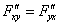 , значит, данное уравнение является уравнением в полных дифференциалах.
, значит, данное уравнение является уравнением в полных дифференциалах.
На чистовике проверка проводится немного не так. Мы не имеем права использовать букву 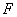 , так как изначально не знаем, является ли данное уравнение полным дифференциалом некоторой функции
, так как изначально не знаем, является ли данное уравнение полным дифференциалом некоторой функции 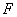 . А вдруг не является? Тогда вышеприведенные записи с буквой
. А вдруг не является? Тогда вышеприведенные записи с буквой 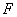 будут некорректны с математической точки зрения. Поэтому обычно используют нейтральные буквы «пэ» и «ку», а сама проверка на чистовике выглядит примерно так:
будут некорректны с математической точки зрения. Поэтому обычно используют нейтральные буквы «пэ» и «ку», а сама проверка на чистовике выглядит примерно так:
“
Проверим, является ли уравнение 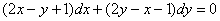 уравнением в полным дифференциалах:
уравнением в полным дифференциалах:
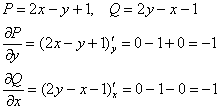
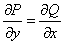 , значит, данное ДУ является уравнением в полных дифференциалах
, значит, данное ДУ является уравнением в полных дифференциалах
”
Вот только теперь, после доказательства, мы можем использовать букву «эф», поскольку показано, что дифференциальное уравнение 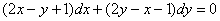 является полным дифференциалом некоторой функции
является полным дифференциалом некоторой функции 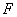 и имеет вид:
и имеет вид:
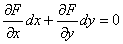
Ну, а коль скоро уравнение 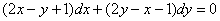 имеет вид
имеет вид 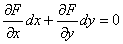 , то:
, то:
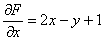
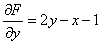
Таким образом, нам известны две частные производные, и наша задача состоит в том, чтобы восстановить общий интеграл 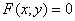 .
.
Существуют два зеркальных способа решения. В статье я остановлюсь на более привычном способе решения, но в конце рассмотрю и второй зеркальный вариант, он не менее важен.
Действие второе. Работаем с верхней производной 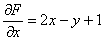 . Нижнюю производную
. Нижнюю производную 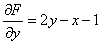 пока запишем на листочек и спрячем в карман.
пока запишем на листочек и спрячем в карман.
Если дана частная производная 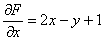 , то нужная нам функция
, то нужная нам функция 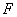 восстанавливается с помощью обратного действия – частного интегрирования:
восстанавливается с помощью обратного действия – частного интегрирования:
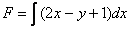
Когда мы берём интеграл по «икс», то переменная «игрек» считается константой. Как видите, принцип точно такой же, как и при нахождении частных производных.
Я запишу подробно, сначала используем свойства линейности интеграла:

Еще раз подчеркиваю, что «игрек» в данном случае является константой и выносится за знак интеграла (т.е. не участвует в интегрировании).
В итоге:
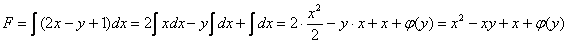
Здесь 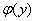 – некоторая, пока ещё неизвестная функция, зависящая только от «игрек».
– некоторая, пока ещё неизвестная функция, зависящая только от «игрек».
Правильно ли вычислен интеграл? В этом легко убедиться, если выполнить проверку, т.е. найти частную производную:
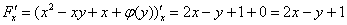 – получена исходная подынтегральная функция.
– получена исходная подынтегральная функция.
Надеюсь всем, понятно, почему 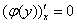 . Функция
. Функция 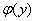 зависит только от «игрек», а, значит, является константой.
зависит только от «игрек», а, значит, является константой.
Действие третье.
Берем «недоделанный» результат 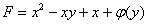 и дифференцируем его по «игрек»:
и дифференцируем его по «игрек»:
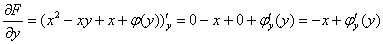
Функцию 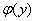 мы пока не знаем, но производная-то по «игрек» у неё существует, поэтому запись
мы пока не знаем, но производная-то по «игрек» у неё существует, поэтому запись 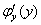 – совершенно законна.
– совершенно законна.
Действие четвертое.
Перепишем результат предыдущего пункта: 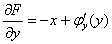
А теперь достаем из широких штанин листочек с производной:
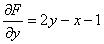
Приравниваем:
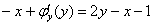
И сокращаем всё, что можно сократить:
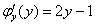
Находим функцию 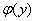 , для этого необходимо взять интеграл от правой части:
, для этого необходимо взять интеграл от правой части:
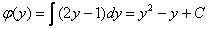
Заключительный аккорд: Подставим найденную функцию 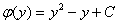 в «недоделанный» результат
в «недоделанный» результат 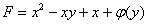 :
:
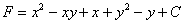
Ответ: общий интеграл: 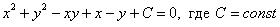
Проверка уже выполнена в самом начале урока – находим частные производные первого порядка и составляем полный дифференциал, в результате должно получиться исходное дифференциальное уравнение.
Второй способ проверки состоит в том, чтобы найти производную от функции, заданной неявно:
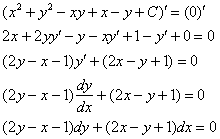
Пример 2
Решить дифференциальное уравнение 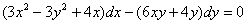
Решение:
1) Проверим, является ли данное ДУ уравнением в полных дифференциалах:
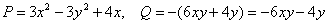
! Не теряем минус при записи 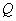 !
!
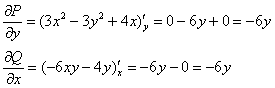
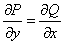 , значит, уравнение
, значит, уравнение 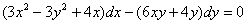 является уравнением в полных дифференциалах и имеет вид:
является уравнением в полных дифференциалах и имеет вид:
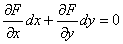
2) Запишем частные производные:
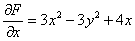 – будем работать с этой производной.
– будем работать с этой производной.
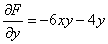 – про эту производную пока забываем.
– про эту производную пока забываем.
Если 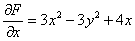 , то:
, то:

где 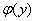 – некоторая, пока ещё неизвестная функция, зависящая только от «игрек».
– некоторая, пока ещё неизвестная функция, зависящая только от «игрек».
Напоминаю, что, когда мы интегрируем по «икс», то переменная «игрек» считается константой и выносится за знак интеграла.
3) Берём «недоделанный» результат предыдущего пункта 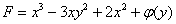 и дифференцируем его по «игрек»:
и дифференцируем его по «игрек»:
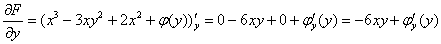
4) Переписываем найденный результат: 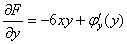
А теперь вспоминаем про «забытую» в начале второго пункта производную:
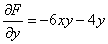
Приравниваем и сокращаем:
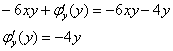
Примечание: На практике решение обычно записывают значительно короче, объединяя пункты №№3,4:
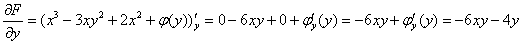 , то есть сразу же после нахождения производной приравнивается «забытая» производная. В последнем равенстве
, то есть сразу же после нахождения производной приравнивается «забытая» производная. В последнем равенстве 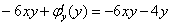 проводятся сокращения, откуда следует:
проводятся сокращения, откуда следует: 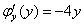 .
.
Восстанавливаем функцию 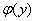 интегрированием по «игрек»:
интегрированием по «игрек»:
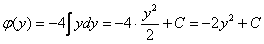
В «недоделанный» результат 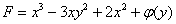 пункта №2 подставляем найденную функцию
пункта №2 подставляем найденную функцию 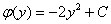 .
.
Ответ: общий интеграл: 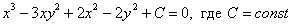
Ответ можно записать и в стандартном виде 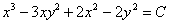 , но здесь возникает любопытная особенность, о которой я рассказывал на уроке Дифференциальные уравнения первого порядка. Если мы переносим константу в правую часть, то, строго говоря, у неё необходимо сменить знак:
, но здесь возникает любопытная особенность, о которой я рассказывал на уроке Дифференциальные уравнения первого порядка. Если мы переносим константу в правую часть, то, строго говоря, у неё необходимо сменить знак: 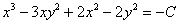 . Константу
. Константу 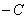 (поскольку она может принимать любые значения) желательно переобозначить некоторой другой константой
(поскольку она может принимать любые значения) желательно переобозначить некоторой другой константой 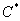 и записать общий интеграл в виде
и записать общий интеграл в виде 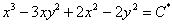 . Если же записать ответ в виде
. Если же записать ответ в виде 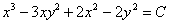 , то формально это будет ошибкой, а неформально – нет. Чтобы избежать лишних телодвижений с переобозначением константы или небрежности в оформлении, лично я предпочитаю оставлять ответ в виде
, то формально это будет ошибкой, а неформально – нет. Чтобы избежать лишних телодвижений с переобозначением константы или небрежности в оформлении, лично я предпочитаю оставлять ответ в виде 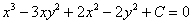
Выполним проверку. Найдём частные производные первого порядка:
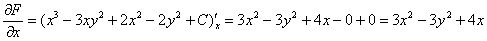
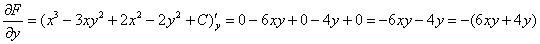
Составим дифференциальное уравнение 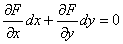 :
:
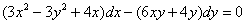
Получено исходное ДУ, значит, задание выполнено правильно.
Пример 3
Решить дифференциальное уравнение 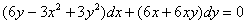
Это пример для самостоятельного решения. Полное решение в конце урока я записал максимально коротко без пунктов, то есть приблизил его к «боевым» условиям – примерно так нужно оформлять задачу на практике.
Многочлены хорошо, а другие функции – лучше. Рассмотрим еще пару примеров.
Пример 4
Найти общий интеграл дифференциального уравнения.
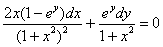
Решение: Проверим, является ли данное ДУ уравнением в полных дифференциалах:
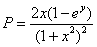 ,
, 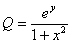
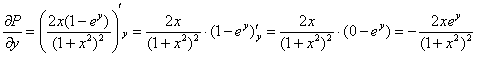
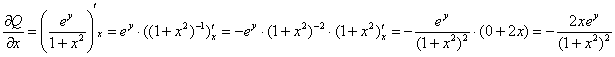
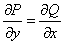 , значит, данное дифференциальное уравнение является уравнением в полных дифференциалах и имеет вид:
, значит, данное дифференциальное уравнение является уравнением в полных дифференциалах и имеет вид:
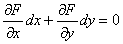
Запишем частные производные первого порядка:
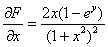 – работаем с этой производной
– работаем с этой производной
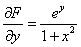 – про эту производную пока забываем
– про эту производную пока забываем
Если 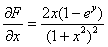 , то:
, то:
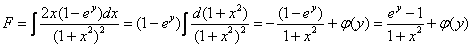
Здесь 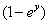 является константой, которая вынесена за знак интеграла, а сам интеграл найден методом подведения функции под знак дифференциала.
является константой, которая вынесена за знак интеграла, а сам интеграл найден методом подведения функции под знак дифференциала.
Находим частную производную по «игрек»:
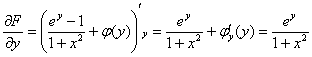
Это стандартное короткое оформление задания, когда после нахождения производной сразу приравнивается «забытая» производная 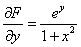 .
.
Из последнего равенства 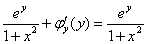 после сокращения следует, что
после сокращения следует, что 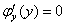 , это простейший случай:
, это простейший случай:
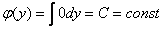
Подставляем найденную функцию 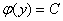 в «недоделанный» результат
в «недоделанный» результат 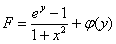
Ответ: общий интеграл: 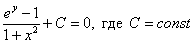
Пример 5
Найти общий интеграл дифференциального уравнения.
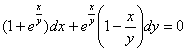
Это пример для самостоятельного решения, заодно проверите свои навыки в нахождении частных производных. Полное решение и ответ в конце урока.
А сейчас я рассмотрю обещанный зеркальный метод решения. Обязательно с ним ознакомьтесь, пригодится не только в диффурах, но и некоторых других задачах матана.
Пример 6
Найти общий интеграл дифференциального уравнения.
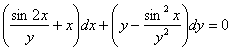
Решение:
Начало решения точно такое же, необходимо убедиться, что перед нами уравнение в полных дифференциалах:
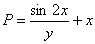 ,
, 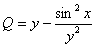
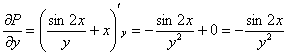
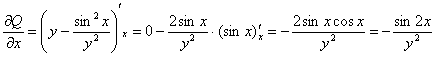
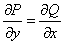 , значит, данное дифференциальное уравнение является уравнением в полных дифференциалах и имеет вид:
, значит, данное дифференциальное уравнение является уравнением в полных дифференциалах и имеет вид:
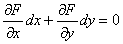
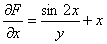 – про эту производную пока забываем.
– про эту производную пока забываем.
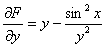 – будем работать с этой производной.
– будем работать с этой производной.
Отличие состоит в том, что пляска начинается от другой производной. Может показаться, что второй способ «рассматривать не обязательно», но время от времени выручает именно он. Когда? Когда вы пытаетесь стандартно начать решение с верхней производной 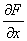 , но в результате получается очень трудный интеграл. В такой ситуации всегда следует попробовать начать решение с нижней производной
, но в результате получается очень трудный интеграл. В такой ситуации всегда следует попробовать начать решение с нижней производной 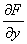 , вполне возможно, что интеграл получится значительно проще.
, вполне возможно, что интеграл получится значительно проще.
Итак, если 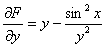 , то:
, то:
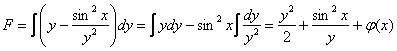
Восстановление общего интеграла 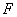 проведено частным интегрированием по «игрек».
проведено частным интегрированием по «игрек».
Когда мы берём интеграл по «игрек», то переменная «икс» считается константой. Именно поэтому константа 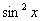 вынесена за знак интеграла и не принимает участия в интегрировании.
вынесена за знак интеграла и не принимает участия в интегрировании.
Функция 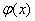 зависит только от «икс» и пока ещё неизвестна.
зависит только от «икс» и пока ещё неизвестна.
Теперь находим частную производную по «икс»:
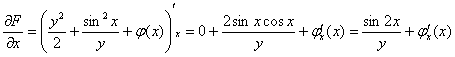
Вспоминаем о «забытой» производной: 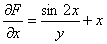
Приравниваем результаты и проводим сокращения:
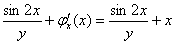
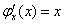
Функцию 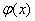 восстанавливаем интегрированием:
восстанавливаем интегрированием:
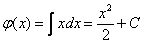
Найденную функцию 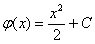 подставляем в недостроенный общий интеграл
подставляем в недостроенный общий интеграл 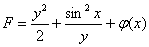
Ответ: общий интеграл: 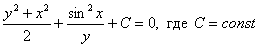
Вторым способом можно было решить все примеры, которые мы рассмотрели до этого. Оба способа решения абсолютно равноценны, используйте тот, который вам удобнее.
Пример 7
Решить дифференциальное уравнение
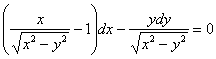
Это пример для самостоятельного решения. Решение в образце проведено вторым способом.
Заканчиваю печатать эту статью и обращаю внимание на то, что она получилась неожиданно большой. Когда материалы по диффурам в полных дифференциалах были только в моих планах, думал, урок получится меньше по объему раза в два. Что делать, присутствует новый материал – частное интегрирование. А новый материал в две строчки не уместишь.
Существуют еще так называемые уравнения, сводящиеся к уравнениям в полных дифференциалах. Они решаются методом интегрирующего множителя. В моей практике такие уравнения встречались, но всего 2-3 раза, и я не счел целесообразным включать их в методические материалы. Если возникнет необходимость рассмотреть метод интегрирующего множителя, пожалуйста, обратитесь к специализированной литературе по диффурам, в частности, можно воспользоваться решебником Обыкновенные дифференциальные уравнения, авторы – М.Л. Киселёв, А.И. Киселёв, Г.И. Макаренко. Разберётесь легко, поскольку такое уравнение могут предложить только по причине хорошей успеваемости =)
Надеюсь, объяснения были достаточно подробны и понятны.
Полного вам дифференциала!
Решения и ответы:
Пример 3: Решение: 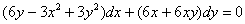
Проверим, является ли данное ДУ уравнением в полным дифференциалах:
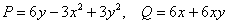
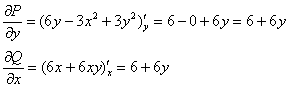
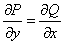 , значит, данное уравнение является уравнением в полных дифференциалах:
, значит, данное уравнение является уравнением в полных дифференциалах:
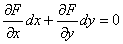
Таким образом:
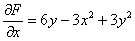
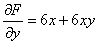
Если 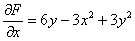 , то:
, то:
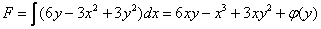
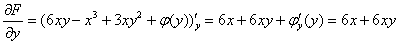
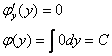
Ответ: общий интеграл: 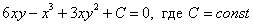
Пример 5: Решение: Проверим, является ли данное ДУ уравнением в полным дифференциалах:
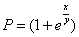 ,
, 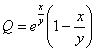
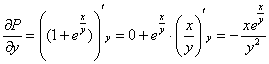
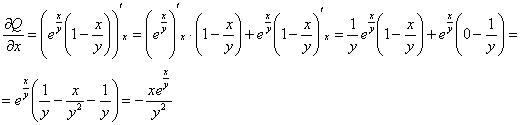
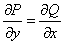 , значит, данное ДУ является уравнением в полных дифференциалах и имеет вид:
, значит, данное ДУ является уравнением в полных дифференциалах и имеет вид:
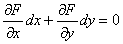
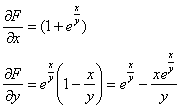
Если 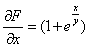 , то:
, то:
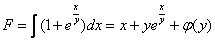
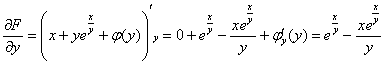
В последнем равенстве всё сократилось:
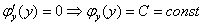
Ответ: общий интеграл: 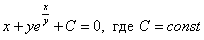
Пример 7: Решение:
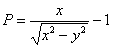 ,
, 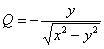
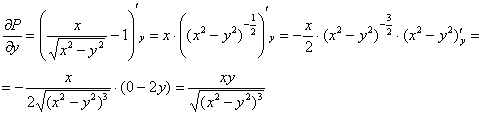
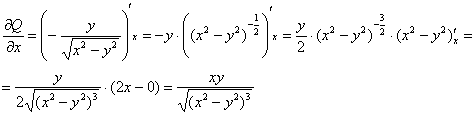
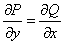 , значит, данное ДУ является уравнением в полных дифференциалах и имеет вид:
, значит, данное ДУ является уравнением в полных дифференциалах и имеет вид:
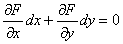
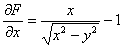
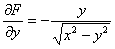
Если 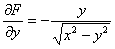 , то:
, то:
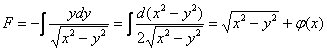
Находим частную производную по «икс»:
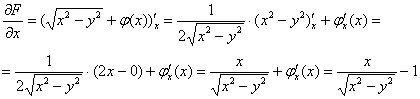
Из последнего равенства 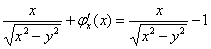 после сокращений получаем:
после сокращений получаем:
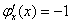
Найдем 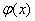 :
:
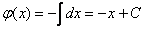
Подставим найденную функцию 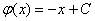 в недостроенный общий интеграл
в недостроенный общий интеграл 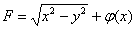
Ответ: общий интеграл: