Поверхностный интеграл второго рода, его свойства

Пусть задана поверхность S, ограниченная линией L (рис. 3.10).

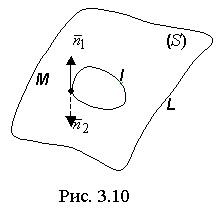
Возьмём на поверхности S какой-нибудь контур l, не имеющий общих точек с границей L.

В точке М контура l можно восстановить две нормал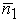и и 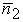к поверхности S.

Выберем какое-либо одно из этих направлений.

Обводим точку М по контуру l с выбранным направлением нормали.

Если в исходное положение точка М вернётся с тем же направлением нормали (а не с противоположным), то поверхность S называют двусторонней.

Мы будем рассматривать только двусторонние поверхности
Двусторонней поверхностью является всякая гладкая поверхность с уравнением z = f(x,y).

Пусть S - двусторонняя незамкнутая поверхность, ограниченная линией L, не имеющей точек самопересечения. Выберем определённую сторону поверхности.

Будем называть положительным направлением обхода контура L такое направление, при движении по которому по выбранной стороне поверхности сама поверхность остаётся слева.

Двусторонняя поверхность с установленным на ней таким образом положительным направлением обхода контуров называется ориентированной поверхностью.

Перейдём к построению поверхностного интеграла второго рода. Как при изучении криволинейных интегралов второго рода рассматривалась направленная кривая, так и при построении поверхностного интеграла второго рода рассматривается определенная сторона поверхности.

Возьмём в пространстве двустороннюю поверхность S, состоящую из конечного числа кусков, каждый из которых задан уравнением видаz = f(x,y) или является цилиндрической поверхностью с образующими, параллельными оси Oz.

Пусть R(x,y,z) - функция, опредёленная и непрерывная на поверхности S. Сетью линий разбиваем S произвольным образом на n "элементарных" участков ΔS₁, ΔS₂, ..., ΔS_i, ..., ΔS_n, не имеющих общих внутренних точек.

На каждом участке ΔS_i произвольным образом выберем точку M_i(x_i,y_i,z_i) (i=1,...,n). Пусть (ΔS_i)_xy - площадь проекции участка ΔS_i на координатную плоскость Оху, взятая со знаком "+", если нормаль к поверхности S в точке M_i(x_i,y_i,z_i) образует с осью Oz острый угол, и со знаком "-", если этот угол тупой.

Составим сумму 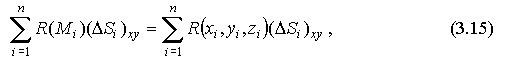которую называют интегральной суммой для функции R(x,y,z) по поверхности S по переменным х, у.

Обозначим λ - наибольший из диаметров ΔS_i (i = 1, ..., n).

Если существует конечный предел ,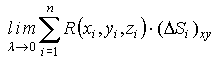

не зависящий от способа разбиения поверхности S на "элементарные" участки ΔS_i и от выбора точек M_i 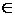ΔS_i (i = 1, ..., n), то он называется поверхностным интегралом по выбранной стороне поверхности S от функции R(x,y,z) по координатам х, у (или поверхностным интегралом второго рода) и обозначается

Аналогично можно построить поверхностные интегралы по координатам x, z илиу, z по соответствующей стороне поверхности, т. е.

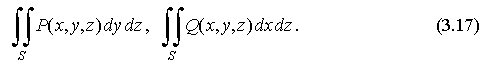
Если существуют интегралы (3.16) и (3.17), то можно ввести "общий" интеграл по выбранной стороне поверхности:

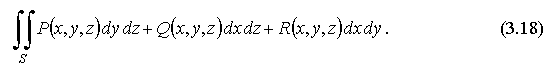
Поверхностный интеграл второго рода обладает обычными свойствами интеграла. Заметим лишь, что любой поверхностный интеграл второго рода изменяет знак при перемене стороны поверхности.

Вычисление интеграла (3.16) как правило, сводят к вычислению двойного интеграла.

Пусть S - двусторонняя поверхность, заданная уравнением z=f(x,y), где f(x,y) непрерывна в области τ (τ есть проекция поверхности S на координатную плоскость Оху), и R(x,y,z) - непрерывная функция на поверхности S.

Выберем "верхнюю" сторону поверхности S, тогда знак проекции (ΔS_i)_xy всегда "+", поэтому

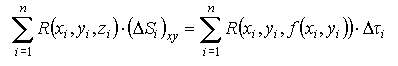есть интегральная сумма для функции R(x,y,f(x,y)) по плоской области τ.

Переходя к пределу (приλ 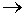0 ), получаем 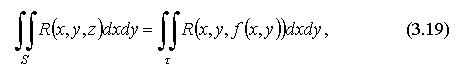отсюда и очевидны условия существования поверхностного интеграла второго рода.

*************************************