Способы задания функции

Предисловие

Современное естествознание вступило в эру количественных и точных методов познания жизненных процессов. Одним из примеров этого является активное развитие математического моделирования в биологии и медицине с широким привлечением компьютеров и прикладных программ.

Очевидно, что без знания основных математических понятий и законов невозможно глубокое изучение физических, физико-химических и физиологических процессов, обеспечивающих жизнедеятельность организма, понимание сущности математического моделирования и др.

Трудности, возникающие при решении конкретных количественных биологических и медицинских задач связаны, как правило, с пробелами знаний в различных разделах математики.

Настоящее учебное пособие разработано авторами с учетом опыта преподавания курса медицинской и биологической физики. В пособии очень кратко излагаются некоторые темы из курса элементарной математики, знание которых необходимо для понимания дальнейшего теоретического материала высшей математики. Кроме того к каждому разделу даны примеры и задачи и показаны способы их решения.

Более подробно рассмотрены колебательные процессы и вопросы математического моделирования в медицине и биологии.

ГЛАВА 1. Краткие сведения из элементарной математики.

Функция

При изучении различных явлений природы и решении целого ряда задач приходится рассматривать изменение одной величины в зависимости от изменения другой. Так, например, пройденный телом путь мы рассматриваем, как величину переменную, изменяющуюся в зависимости от времени, т.е. пройденный путь есть функция времени.

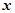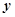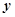Определение 1. Если каждому значению переменной , принадлежащему некоторой области, соответствует одно определенное значение другой переменной , то есть функция от 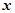, т.е. .

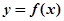Переменная 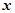называется независимой переменной или аргументом.

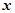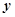Зависимость переменных и называется функциональной зависимостью.

Определение 2. Совокупность значений 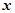, для которых определяются значения функции в силу правила 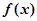, называется областью определения функции.

Способы задания функции

I. Табличный способ задания функции

При этом способе выписываются в определенном порядке значения аргумента 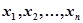и соответствующие значения функции .

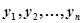x	x1	x2	...	xn
y	y1	Y2	...	Yn

Таковы, например, таблицы тригонометрических функций.

В результате экспериментального изучения физических явлений, как правило, получаются таблицы, выражающие функциональную зависимость между измеряемыми величинами.

II. Графический способ задания функции

Если в прямоугольной системе координат на плоскости имеем некоторую совокупность точек 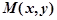, при этом никакие две точки не лежат на одной прямой, параллельной оси 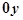, то эта совокупность точек определяет некоторую однозначную функцию 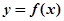, где значениями аргумента являются абсциссы точек, значениями функции - соответствующие ординаты.

Совокупность точек плоскости 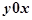, абсциссы которых являются значениями независимой переменной, а ординаты - соответствующими значениями функции, называется графиком данной функции.

III. Аналитический способ задания функции

Аналитическим выражением называется символическое обозначение совокупности математических операций, которые необходимо произвести в определенной последовательности над числами и буквами, обозначающими постоянные или переменные величины.

Если функциональная зависимость 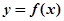такова, что 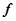обозначает аналитическое выражение, то значит, что функция 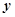от 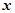задана аналитически.

Например: 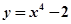, , 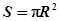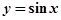и т. д.

IV. Параметрический способ задания функции

Даны два уравнения: ,

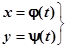где каждому значению 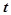соответствуют значения 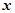и 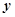. Эти уравнения называются параметрическими, 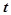- параметром. Часто уравнения некоторых кривых задают в параметрической форме. Например:

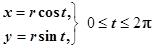
Это есть параметрические уравнения окружности. Если мы исключим из этих уравнений параметр 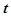, то получим уравнение окружности, содержащее только 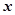и 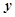. Возводя в квадрат параметрические уравнения и складывая, находим:

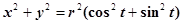или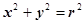

Можно также параметрически задать уравнение эллипса:

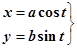или