Урок № 64. Тема 6.8. Решение задач

План занятия.

Решить задачи.

Задача 1. Из точки отстающей от плоскости на 5 дм проведены под углом 30⁰ к плоскости две наклонные, их проекции составляют между собой угол 120⁰. Определить расстояние между основаниями наклонных. (Ответ. 15 дм.)

Задача 2. Катеты прямоугольного треугольника равны 120 см и 16 см. из вершины прямого угла С восстановлен перпендикуляр СД, равный 9,6 см. Определить расстояние от точки Д до гипотенузы. (Ответ.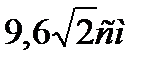

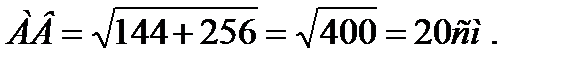
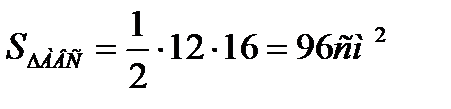
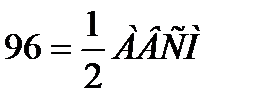
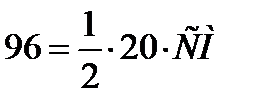
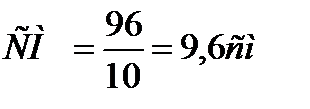
|ДМ|= 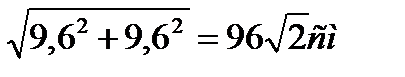|ДМ|=9,6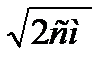

Задача 3. Стороны ∆АВС равны 10 см, 17см., 21 см. Из вершины большого угла А проведен перпендикуляр АД к плоскости ∆АВС длиной 15 см. Определить расстояние от точки Д до стороны ВС.

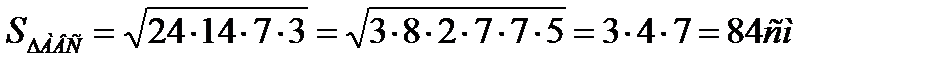
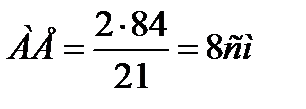|АЕ|=8 см.

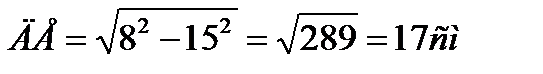
(Ответ. |ДЕ|=17см.)

Задача 4. Дан ∆АВС со сторонами |АВ|=9 см., |АС|=5см, |ВС|=6см. Через сторону АС проходит плоскость α, составляющая с плоскостью треугольника угол 45⁰. Найти расстояние между плоскостью α и вершиной В.

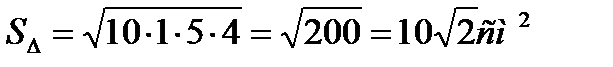
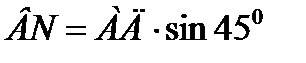
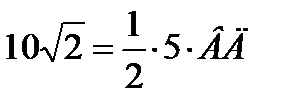
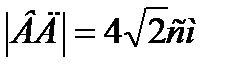
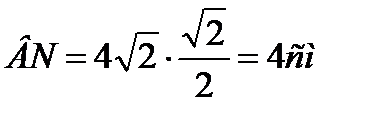
(Ответ. |BN|=4см.)

Домашнее задание

1) Выучить все теоремы.

2) Задача 1. ∆АВС равносторонний АВ=ВС=АС=8 см. Из вершины А восстановлен перпендикуляр АД к плоскости ∆АВС. Определить расстояние от точки Д до стороны ВС.

(Ответ. 8 см.)

Задача 2. Из точки А проведены две наклонные, каждая из которых равна 12 см и наклонена под углом 450. Определить расстояние между основаниями наклонных, если угол между их проекциями прямой. (Ответ. 12 см.)

Задача 3. Концы отрезка MN удалены от плоскости на 3 см и 5 дм. Как удалена от плоскости точка, делящая отрезок MN в отношении 1:3. (Ответ. 4,5 см.).

Урок № 65. Тема 7.1.: Векторы на плоскости.

План занятия.

1. Определение вектора.

2. Обозначение вектора.

3. Изображение вектора.

4. Равенство векторов.

5. Координаты вектора.

х₂ – х₁=а₁

у₂-у₁=а₂

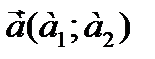или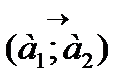

Расстояние между двумя точками

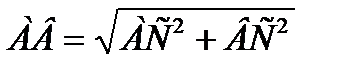
|АВ|=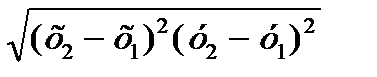

Длина вектора (модуль вектора)

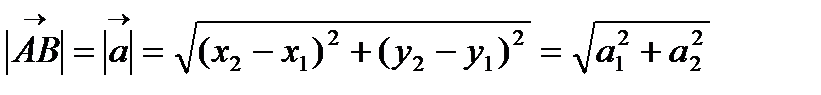
Координаты середины отрезка.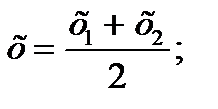

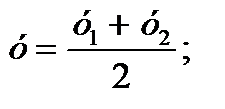
Действие над векторами.

Сложение.

а) геометрически (способы параллелограмма, треугольника, многоугольника).

б) аналитически.

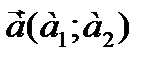
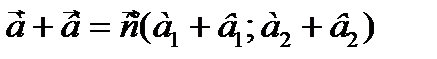
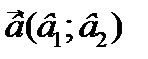
Вычитание

а) геометрически (методом треугольника)

б) аналитически.

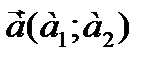
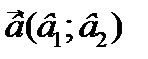
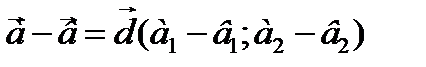
Умножение вектора на число

а) геометрические

б) аналитические

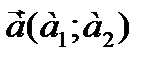
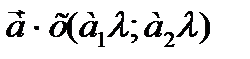
Скалярное произведение

Определение. Скалярным произведением двух векторов 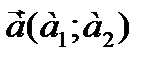, 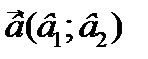называется число

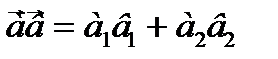
Пример: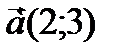

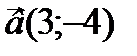
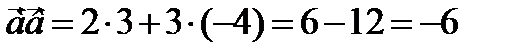
Теорема. Скалярное произведение двух векторов равно произведению их абсолютных величин на косинус угла между ними.

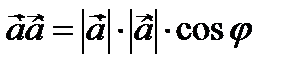
Угол между двумя векторами

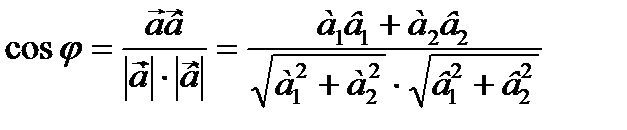
Определение. Два отличных от нуля вектора называются коллинеарными, если они не лежат на одной прямой или на параллельных прямых.

Разложение вектора по координатным осям

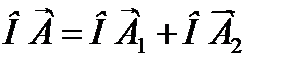
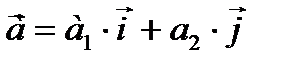
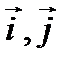- единые векторы для осей х, у (орты).

Закрепление нового материала.

Домашнее задание: выучить конспект.

Урок № 66. Тема 7.2.: Прямоугольные координаты на плоскости и пространстве. Действия над векторами, заданными своими координатами. Длина вектора, угол между векторами.

План занятия.