Неопределенный интеграл

Рассмотрим операцию обратную к дифференцированию, которая называется интегрированием и состоит в отыскании функции по ее производной.

Определение 1. Функция называется первообразной функции на промежутке , если дифференцируема на этом промежутке и

Определение 2. Множество всех первообразных функции на промежутке называется неопределенным интегралом от функции на множестве и обозначается .

Теорема.Если есть первообразная функции на промежутке , то

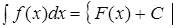R. (1)

Доказательство.

Очевидно, что также есть первообразная на .Пусть другая первообразная. Тогда . Поэтому и

Теорема доказана.

Обычно формулу (1) записывают в следующем виде:

=.

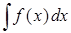Из таблицы производных получается таблица неопределенных интегралов:

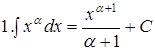
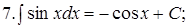
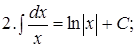
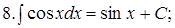
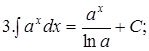
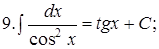
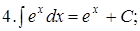
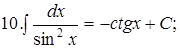
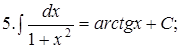
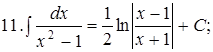
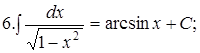
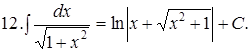
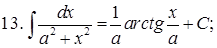
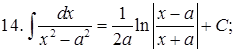
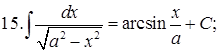
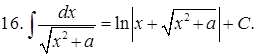
Эти формулы легко доказать непосредственным дифференцированием.

Замечание 1.Все неопределенные интегралы в таблице рассматриваются на промежутках, на которых определены все функции, входящие в соответствующую формулу.

Замечание 2.Второй табличный интеграл представляет собой две формулы:

I. На промежутке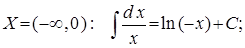

II. На промежутке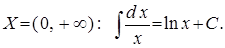

Из формулы (1) и свойств производной получаются следующие правила интегрирования, которые мы сформулируем в виде теорем.

Теорема 1. Постоянный множитель можно вынести за знак интеграла:

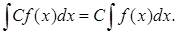
Теорема 2. Интеграл от суммы или разности равен сумме или разности интегралов:

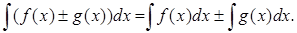
Доказательства теорем 1 и 2 получаются непосредственно из определения 2 и соответствующих свойств производной.

Пример 1.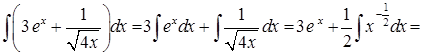

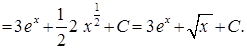
Следуещее правило часто испульзуется, если под знаком интеграла стоит произведение функций.

Теорема 3. Пусть функции 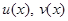и их производные 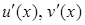непрерывны на промежутке X. Тогда на этом промежутке

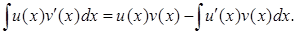(2)

Доказательство.

Из правила дифференцирования произведения функций выразим

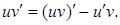
Тогда из теоремы 2 получим

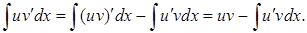
Теорема доказана.

Замечание 1. Формула (2) называется формулой интегрирования по частям. Из определения дифференциала функций следуют равенства:

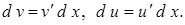
Отсюда и из (2) получим формулу интегрирования по частям в дифференциальной форме:

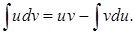(3)

Замечание 2.При использовании формулы (3) полезна таблица дифференциалов, которая в ходе решения задач читателями может быть расширена:

Таблица внесения функций под знак дифференциала.

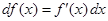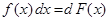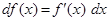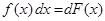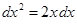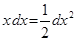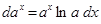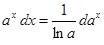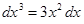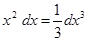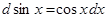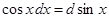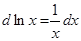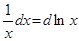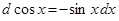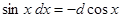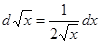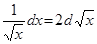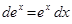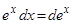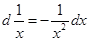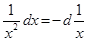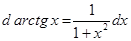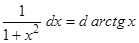Замечание 3. При выборе функций u и v в формуле интегрирования по частям рекомендуется использовать следующие соображения. Пусть подынтегральная функция представлена в виде произведения двух функций. Тогда в качестве функции u нужно взять ту из них, которая упростится после взятия производной. Оставшийся множитель следует внести под знак дифференциала (при этом можно использовать таблицу дифференциалов). Функция, оказавшаяся после этого под знаком дифференциала, будет являться функцией v.

Пример.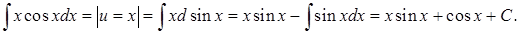

Теорема 4.Пусть функция f (u) непрерывна на промежутке U, а функция u=φ(x) отображает промежуток X в промежуток U и 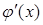существует и сохраняет постоянный знак на промежутке X. Тогда на X

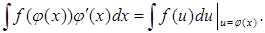(4)

Доказательство.

Пусть F(u) есть первообразная функция f(u) на промежутке U. Тогда

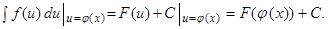(5)

По правилу дифференцирования сложной функции имеем

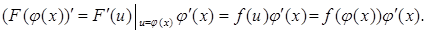
Поэтому 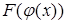есть первообразная 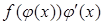на промежутке X и

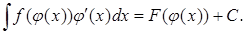(6)

Из (5) и (6) следует (4). Теорема доказана.

Замечание 4.Формула (4) называется формулой замены переменной. Для того, чтобы пользоваться таблицей дифференциалов, эту формулу удобно применять в следующей форме:

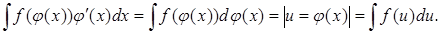(7).

Замечание 5.При использовании формулы (7) можно применять следующие свойства дифференциала:

I. Постоянный множитель можно вынести из под знака дифференциала;

II. Под знаком дифференциала можно прибавить и отнять константу;

III. Дифференциал от суммы или разности функций равен сумме или разности дифференциалов.

Замечание 6.При внесении функции 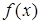под дифференциал под знаком дифференциала получим первообразную функции 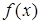. Таким образом, 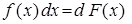, где 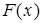есть первообразная функции 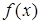( 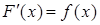), которая может быть найдена с помощью неопределенного интеграла.

Пример.

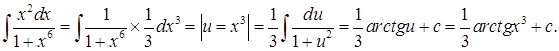
Замечание 7.Формулу замены переменой применяют, если правая часть в формуле (4) вычисляется проще чем левая. В некоторых задачах бывает наоборот: левая часть проще, чем правая. В таких случаях формулу (4) читают справа налево и называют формулой подстановки:

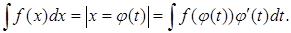(8).

Пример. 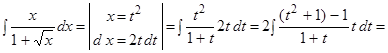.
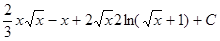