Основные правила дифференциального исчисления. Производные основных функций
Пусть функции 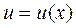 и
и 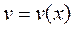 дифференцируемы (т.е. имеют конечные производные), с– постоянная величина, тогда имеют место следующие формулы:
дифференцируемы (т.е. имеют конечные производные), с– постоянная величина, тогда имеют место следующие формулы:
1.  . Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных.
. Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных.
2. 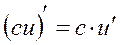 . Постоянный множитель можно выносить за знак производной.
. Постоянный множитель можно выносить за знак производной.
3. 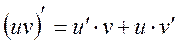 . Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй, плюс произведение производной второго сомножителя на первый.
. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй, плюс произведение производной второго сомножителя на первый.
4. 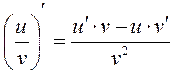 ,
, 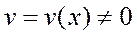 . Если числитель и знаменатель дроби — дифференцируемые функции и знаменатель не обращается в нуль, то производная дроби равна производной числителя, умноженной на знаменатель, минус производная знаменателя, умноженная на числитель, и все это деленное на квадрат знаменателя.
. Если числитель и знаменатель дроби — дифференцируемые функции и знаменатель не обращается в нуль, то производная дроби равна производной числителя, умноженной на знаменатель, минус производная знаменателя, умноженная на числитель, и все это деленное на квадрат знаменателя.
Производные основных функций
 ;
;
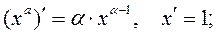
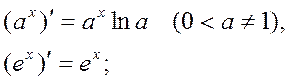
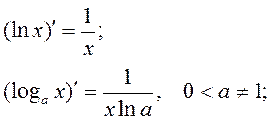
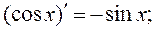
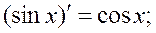
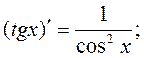
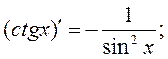
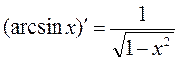 ;
;
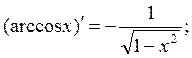
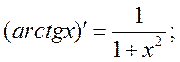
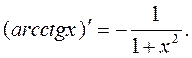
Примеры: Вычислить производные следующих функций
1. f(x)=  ,
,
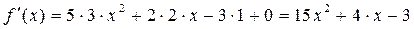 .
.
2. 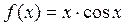 ,
,
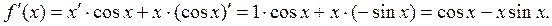
3. 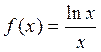 ,
,  .
.
Эластичность.
Понятие эластичности было введено Альфредом Маршаллом в связи с анализом функции спроса. Впоследствии это понятие было распространено и на другие функции.
Эластичностью функции называется предел отношения относительного приращения функции у=f(x) к относительному приращению переменной x если приращение
аргумента стремится к нулю 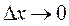 . Эластичность функции обозначается:
. Эластичность функции обозначается: 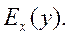
 т.е.
т.е. 
Вывод: эластичность — это коэффициент пропорциональности между относительными изменениями величин у и х. Если, например, х увеличится на один процент, то у увеличится (приближенно) на  процентов.
процентов.
Эластичность спроса относительно цены.Пусть спрос q зависит от цены p по закону  . Функция
. Функция 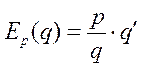 показывает, как изменится спрос на данный товар, если цена изменится на 1%. Так как обычно
показывает, как изменится спрос на данный товар, если цена изменится на 1%. Так как обычно 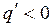 , т.е. с увеличением цены спрос уменьшается, то
, т.е. с увеличением цены спрос уменьшается, то 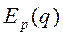 берут со знаком «-», т.е.
берут со знаком «-», т.е.
 .
.
Если 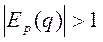 , то говорят, что спрос эластичен, а если
, то говорят, что спрос эластичен, а если 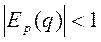 , то неэластичен, если же
, то неэластичен, если же 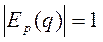 , то спрос нейтрален.
, то спрос нейтрален.
Эластичность предложения относительно цены.Пусть количество товара s, предлагаемого на продажу в единицу времени, зависит от цены p по закону 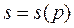 . Функция
. Функция 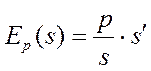 показывает, как изменится предложение, если цена на товар изменится на 1%.
показывает, как изменится предложение, если цена на товар изменится на 1%.
Пример. Правильное применение знаний об эластичности спроса на товары помогает правительству в оценке последствий введения новых налогов или акцизов. Пусть х — акцизы на водку, у — спрос на этот товар. Предположим, что государство предполагает повысить акцизы на водку на 10%. Если известно, что эластичность спроса составляет 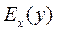 =—0,2, то следует ожидать, что это вызовет снижение спроса на данный товар на 0,2•10=2 (%) и доходы государства по продаже водки повысятся на 8%.
=—0,2, то следует ожидать, что это вызовет снижение спроса на данный товар на 0,2•10=2 (%) и доходы государства по продаже водки повысятся на 8%.
Пример. Найти эластичность спроса q относительно цены p, если 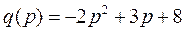 , при p=1, p=32.
, при p=1, p=32.
Решение.Эластичность спроса относительно цены найдём по формуле  . Найдём производную
. Найдём производную
 .
.
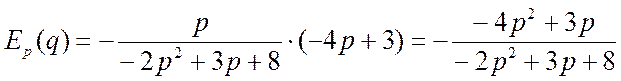
При p=1 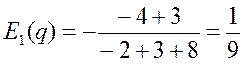 , т.е. спрос неэластичен.
, т.е. спрос неэластичен.
При p=32 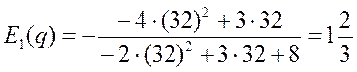 , т.е. спрос эластичен.
, т.е. спрос эластичен.
