Доверительные интервалы для оценки математического ожидания

нормального распределения при неизвестном s

Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение s неизвестно. Требуется оценить неизвестное математическое ожидание а с помощью доверительных интервалов. Разумеется, невозможно воспользоваться результатами предыдущего параграфа, в котором s предполагалось известным.

Можно показать, что доверительный интервал в этом случае имеет вид:

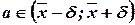, где .

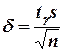Здесь t_g – квантиль распределения Стьюдента, который находится как корень уравнения

.

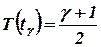Для вычисления t_g можно воспользоваться встроенной функцией табличного процессора MS Excel:

.

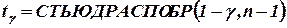При неограниченном возрастании объема выборки п распределение Стьюдента стремится к нормальному. Поэтому практически при n > 30 можно вместо распределения Стьюдента пользоваться нормальным распределением. Однако важно подчеркнуть, что для малых выборок (n < 30), в особенности для малых значений п, замена распределения нормальным приводит к грубым ошибкам, а именно к неоправданному сужению доверительного интервала, т. е. к повышению точности оценки. Например, если n = 5 и g = 0,99, то, пользуясь распределением Стьюдента, найдем t_g= 4,6, а используя функцию Лапласа, найдем t = 2,58, т. е. доверительный интервал в последнем случае окажется более узким, чем найденный по распределению Стьюдента.

Оценка вероятности (биномиального распределения) по относительной частоте

Пусть производятся независимые испытания с неизвестной вероятностью р появления события А в каждом испытании. Требуется оценить неизвестную вероятность р по относительной частоте, т. е. надо найти ее точечную и интервальную оценки.

Точечная оценка. В качестве точечной оценки неизвестной вероятности р принимают относительную частоту

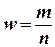
где m - число появлений события А; п - число испытаний.

Эта оценка несмещенная, т. е. ее математическое ожидание равно оцениваемой вероятности. Действительно, учитывая, что М(m) = пр, получим
М(w) = М[m/n] = М(m)/n = nр/n = р.

Найдем дисперсию оценки, приняв во внимание, что D(m) = npq:

D(w) = D[m/n] = D(m)/n² = npq/n² = pq/n.

Отсюда среднее квадратическое отклонение:

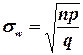
Интервальная оценка. Доверительный интервал для оценки вероятности по относительной частоте имеет вид:

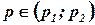, где

,

,

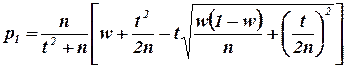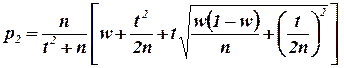где t – квантиль нормированного нормального распределения, который находится из условия:

.

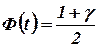При больших значениях n (порядка сотен) слагаемые 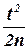и 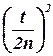очень малы и множитель 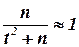, поэтому можно принять в качестве приближенных границ доверительного интервала

.
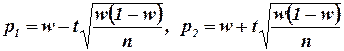