Предельный переход под знаком интеграла Стилтьеса
Пусть функции 
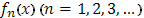непрерывны в промежутке 
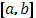и при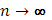 
равномерно стремятся к предельной функции
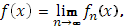
также непрерывной, а 
- функция с ограниченным изменением. Тогда
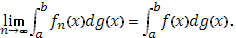
Доказательство:
По заданному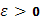 
найдется такое N, что при n
>
N
будет для всех x
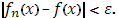
Тогда в силу (21), для n
>
N
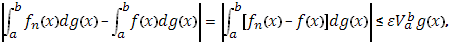
т.к.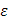 
- произвольное, то теорема доказана.
Пусть функция 
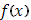непрерывна в промежутке 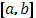, а функция 
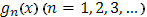- все с ограниченным изменением в этом промежутке. Если полные изменения этих функций в их совокупности ограничены:
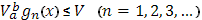
и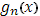 
при 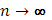стремятся к предельной функции
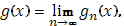
то
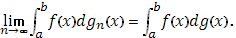
Доказательство:
Докажем, что имеет ограниченное изменение. Разложим промежуток 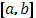произвольным образом на части точками
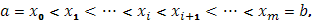
Тогда для любого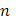 
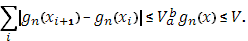
Перейдем к пределу при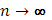
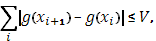
откуда и
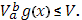
Составим суммы Стилтьеса
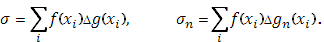
Если предположить, что промежуток 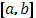при этом разложен на столь мелкие части, что колебание функции 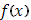в каждой из них будет уже меньше произвольного наперед взятого числа 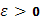, то, в силу оценки (22), при всех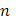
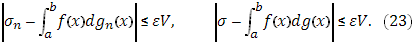
С другой стороны, если разбиение фиксировать, то, очевидно,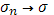 
при 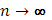, так что найдется такое N
, что для n
>
N будет
Тогда для тех же значений n
в силу (23) и (24) получаем:
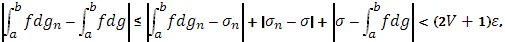
Т.к. 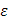- любое, то теорема доказана.
Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
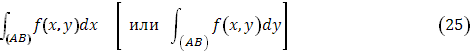
Пусть кривая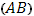 
задана параметрическими уравнениями
в направлении от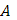 
к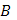 
, когда 
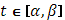. Тогда точкам 
( 
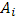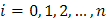), взятым на кривой для образования интегральной суммы, будут отвечать возрастающие значения параметра 
:
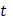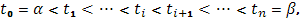
а выбранной на дуг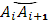е 
точке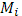 
– значение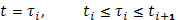 
( 
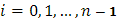). Сама же интегральная сумма, например, для первого из интегралов, напишется в виде
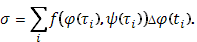
Эта интегральная сумма представляет собою стилтьесову сумму, так что криволинейный интеграл второго типа по самому определению отождествляется с частным случаем интеграла Стилтьеса:
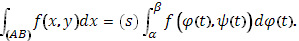
Аналогично и
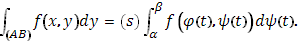
Отсюда следуют общие условия существования криволинейного интеграла (25); достаточно предположить функцию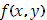 
непрерывной, а функцию 
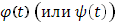имеющей ограниченное изменение (п.3, 
).
В частности, если кривая AB спрямляема, а функции P
(
x
,
y
) и Q
(
x
,
y
) непрерывны, то существует интеграл
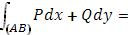
Примеры.
№1 Вычислить по формуле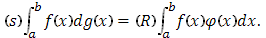 
а)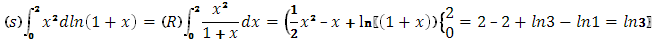 
б
) (s)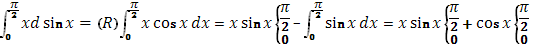 
= 
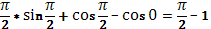
в)(s)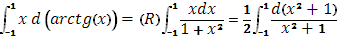 
= 
№2 Вычислить по формуле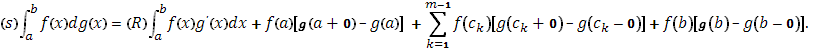 
а)(S)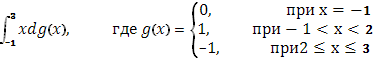 
функция g(x) терпит скачок 1, при х=-1
скачок -2, при х=2
в остальных точках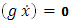 
, т.к. g(x)=const
(S)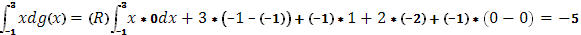 
б
) (S)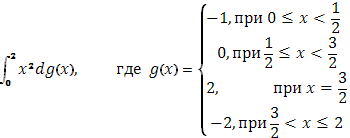 
функция g(x) терпит скачок 1, при х= 
скачок -2, при х=
в остальных точках 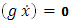, т.к. g(x)=const
(S)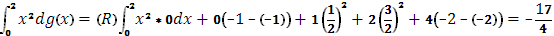 
№3 Вычислить по формуле 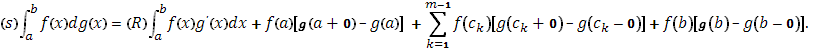При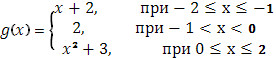 
а)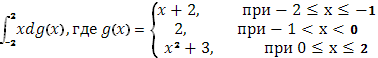 
функция g(x) терпит скачок 1, при х=-1
скачок 1, при х=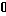 
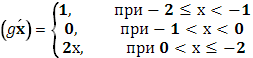
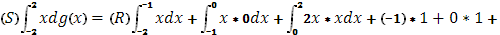
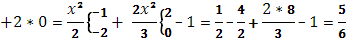
б)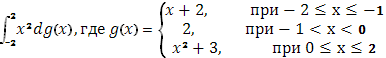 
функция g(x) терпит скачок 1, при х=-1
скачок 1, при х=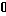
+ 
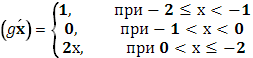
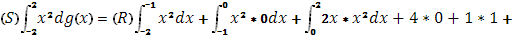
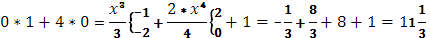
в)
функция g(x) терпит скачок 1, при х=-1
скачок 1, при х=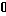
+ 
=
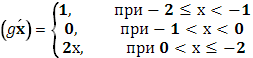
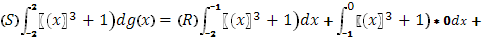
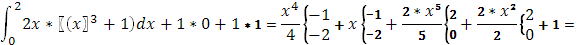
№4
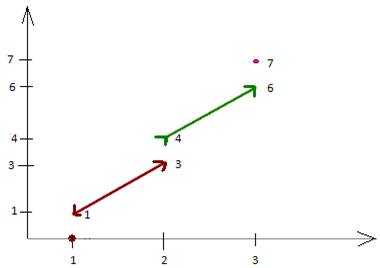
а) Составить выражение Ф(х) и построить график его для следующего распределения масс: массы величины 1 в точках х= 1, 2 и 3 и непрерывно распределенные массы с плотностью 2 в промежутке [1;3]
Решение.
Ф(х)=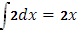 
Ф(а)=о => Ф(1)=0
В точке х=1 функция терпит скачок =1 => Ф(х)=2х-1
В точке х=2 функция терпит скачок =1 => Ф(х)=2х
В точке х=3 функция терпит скачок =1 => Ф(х)=2*3+1=7
Итого:
Ф(х)=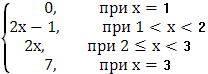 
б) Составить выражение Ф(х) для следующего распределения масс: массы величины 2 в точках х= 2 и 4 и непрерывно распределенные массы с плотностью 2х в промежутке [0;5]
Решение.
Ф(х)=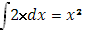 
Ф(а)=о => Ф(1)=0
В точке х=2 функция терпит скачок =2 => Ф(х)=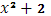 
В точке х=4 функция терпит скачок =2 => Ф(х)= 
Итого:
Ф(х)=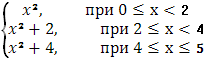 
в) Выяснить распределение масс, если Ф(х)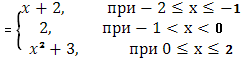 
Решение.
При х=-1 и 0 функция испытывает скачок =1 => массы величины 1 в точках х=-1 и 0, в промежутке [-2,-1] непрерывно распределенные массы с плотностью 1, т.к. , в промежутке [0,2] непрерывно распределенные массы с плотностью 2х, т.к.
Список литературы
1. Г. М. Фихтенгольц. Курс дифференциального и интегрального исчисления. Том 3.Москва 1960
2. http://www.phismat.ru/dif.php