Урок № 55. Тема 5.18. Решение задач
План.
1. Решение упражнений.
2. Контрольная работа.
3. Домашняя работа.
1. Вопросы:
- С помощью какой функции описывается закон равномерного движения?
- С помощью какой функции описывается закон равноускоренного движения?
-какова схема вычисления производной?
-Чему равна производная суммы, произведения, частного?
-что происходит с производной при умножении функции на некоторую постоянную?
-Чему равна производная степенной функции?
-сформулируйте признак постоянства функции
-сформулируйте признак монотонности функции
-сформулируйте необходимое условие экстремума
Сформулируйте достаточное условие экстремума.
Каков алгоритм нахождения промежутков монотонности и точек экстремума?
2. Решение упражнений.
А)Найдите производную функции:
1. 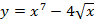
2. 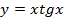
3. 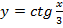
4. 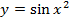
5. 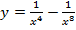
6. 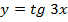
7. 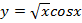
8. 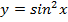
9. 
10. 
Б)Найдите производную функции:
1. 
2. 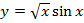
3. 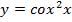
4. 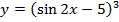
5. 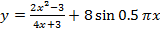
6. 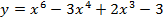
7. 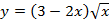
8. 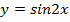
9. 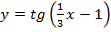
10. 
11. 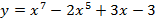
В)Найдите производную функции:
1. 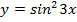
2.y=sin 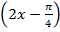
3. 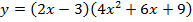
4. 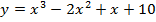
5. 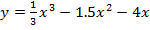
6. 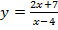
7. 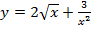
8. 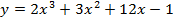
9. 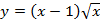
10. 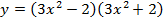
11. 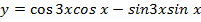
Контрольная работа.
Домашняя работа.
Исследуйте на экстремум следующие функции:

Раздел VI. Прямые и плоскости в пространстве.
Урок № 56. Тема 6.1. Аксиомы стереометрии и следствия из них.
План занятия.
Курс геометрии состоит из планиметрии и сереометрии. Объектами изучения в планиметрии являются фигуры, лежащие в одной и той же плдоскости, например, угол, треугольник, окружность. Поэтому такие фигуры называются плоскими.
В стереометрии изучают фигуры , содержащиеся в пространстве. Среди них имеются неплоские фигуры, например куб, пирамида, цилиндр.
Пространство также содержит все плоские фигуры, поэтому сведения из планимерии понадобятся и в стереометрии.
Изучение стереометрии имеет большое значение для подготовки к практической деятельности. Мы живем и трудимся в трехмерном мире, поэтому усвоение сведений о геометрических фигурах пространства позволяет глубже, полнее осознать свойства реальных предметов, которые создаются природой и людьми.
Курс геометрии основан на определенной системе аксиом.
Аксиомы и следствия из них отражают существенные свойства реального пространства.
С1. Какова ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
С2. Через любые три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну.
С3. Если две точки прямой лежат в плоскости, то и вся прямая лежит в этой плоскости.
С4. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
