Правила составления сетевого графика, термины

При составлении и расчете сетевого графика необходимо выполнять определенные правила, так как в зависимости от тематики и содержания всего комплекса планируемых работ, от принятых единиц измерения, от наличия постоянных, случайных или средних временных оценок могут иметь место разночтения, подмена одних понятий другими, условности и допущения. Примем в данном проекте следующие правила, термины, определения, параметры и приведем расчет.

Работа (или операция) – это любые производственные процессы или иные действия, приводящие к достижению определенных результатов, событий.

Обычно выполнение работ связано с затратами времени, трудовых и материальных ресурсов. Иногда это может быть просто время. Поэтому термин «работа» используется в широком смысле слова и может иметь следующие значения:

· действительная работа – трудовой процесс, требующий затрат времени и ресурсов;

· ожидание – процесс, не требующий затрат труда, но занимающий некоторое время, например, ожидание подписания, согласование документов в различных организациях, ожидание сроков проведения аукционов и другое;

· зависимость – это логическая связь между двумя или несколькими событиями, не требующая затрат труда, материальных ресурсов и времени, но указывающая, что начало одной работы непосредственно зависит от результатов выполнения другой.

Действительные работы изображаются на сетевом графике сплошными стрелками, над или под которыми указывается время для их выполнения; а ожидание и зависимость – пунктирными стрелками.

Стрелки векторного смысла не имеют, а так как сетевой график разворачивается слева направо, то они отображают лишь отношения предшествования и следования: ни одна работа не может быть начата, пока все предшествующие, связанные с ней работы, не будут выполнены. Каждая работа должна иметь свой собственный номер; номер последующей работы должен быть больше номера любой предшествующей работы (см. рис. 5) – связь данной, предшествующей и последующей работ.

Рис. 5. Связь данной, предшествующей и последующей работ.

Событие. Термин используется для обозначения момента времени начала или окончания работы. Событие не требует времени и означает результат выполнения одной или нескольких работ, непосредственно входящих в это событие, позволяющее начинать работы, выходящие из данного события. На сетевом графике событие изображается в виде кружка, внутри которого записывается порядковый номер события.

Исходное событие сети (в данном случае) принято за нулевое. Его номер – 0, оно не имеет входящих в него работ. Завершающее событие сети (в данном случае) имеет номер 16, оно не имеет выходящих из него работ. Всякая работа на сетевом графике соединяет два события: непосредственно предшествующее данной работе и непосредственно за ней следующее. Термины исходное и завершающее событие применяются не только для сетевой модели в целом, но и для любой работы внутри графика, например – см. рис. 5:

· событие Т_i является исходным для работы Т_i-j и, одновременно,

· событие Т_i является завершающим для работы Т_h-i, а

· событие Т_j является исходным для работы Т_j-k и, одновременно,

· событие Т_j является завершающим Т_i-j.

Событие слияния. Термин используется в том случае, когда событие является результатом двух или более входящих в него работ, см. рис. 6.

Рис. 6. Событие слияния.

Т_l – событие слияния, так как оно является результатом выполнения предшествующих, входящих в него трех работ: Т_i-l;Т_j-l;Т_k-l. Эти три работы называются параллельными. По желанию менеджеров, руководящих ходом работ с помощью сетевого графика, они могут выполняться одновременно. Однако, это совсем не обязательно. Все регламентируется результатами анализа, расчета параметров графика и итоговыми данными его оптимизации.

Событие дробления. Термин используется в том случае, когда событие определяет начало двух или более следующих за ним работ, см. рис. 7.

Рис. 7. Событие дробления.

Т_m – событие дробления, так как оно является результатом одной работы Т_l-m и началом трех последующих работ: Т_m-n;Т_m-o;Т_m-p.

Если событие является завершающим для двух или более работ, и одновременно – исходным для двух или более работ, то в расчете параметров сетевого графика при прямом анализе оно называется событием слияния, а при обратном анализе – событием дробления; см. рис. 8.

Рис. 8. Событие слияния-дробления.

Т_d – событие слияния как результат двух входящих в него работ: Т_b-d и Т_c-d; Т_d – событие дробления, как начало трех последующих работ: Т_d-e;Т_d-f; Т_d-h.

Как правило, название работам в сети дается в повелительной форме глагола, например: «Провести экологическую экспертизу земельного участка»; «Представить документы в территориальное управление Росреестра»; «Провести технико-экономическое обоснование мероприятия».и т.п. причем такие названия присваиваются при любом масштабе детализации всех работ и для удобства пользования и расчета параметров сводятся в таблицы.

В расчетно-аналитических таблицах для событий, завершающих указанные работы, записывается соответственно: «Экологическая экспертиза земельного участка проведена»; «Документы из территориального управления Росреестра получены»; «Технико-экономическое обоснование мероприятия проведено».

Путь. Термин используется в том случае, когда требуется определить всякую последовательность работ и связывающих их между собой событий. Путь, соединяющий исходное и завершающее событие сети, считается полным, а все другие - неполными. Каждый путь характеризуется своей продолжительностью, которая равняется сумме длительности составляющих его работ.

Критический путь – это полный путь, имеющий наибольшую продолжительность, от исходного до завершающего события, то есть, это наиболее протяженная по времени последовательная цепочка работ. Для работ, не лежащих на критическом пути, сетевой график определяет резерв времени или ресурса, использованием которого путем соответствующего перераспределения можно сократить общую продолжительность исполнения работ; таким образом, сетевой график обеспечивает получение таких параметров управления, которые позволяют руководящим органам сосредоточитьвсе внимание и имеющиеся ресурсы на выполнении работ, определяющих общее время производства, не распыляя резервы.

Работы и события, лежащие на критическом пути, принято также называть критическими. Полная продолжительность всего комплекса работ, отображенных на сетевом графике, принимается всегда равной критическому пути. Изменение продолжительности любой работы, проходящей через критический путь, соответствующим образом сокращает или удлиняет не только время исполнения промежуточного события, но и срок наступления и завершающего события модели, то есть планируемые сроки осуществления проектирования работ. Поэтому расчетные показатели, характеризующие продолжительность критических работ, а также экономические возможности, которые открываются экономистам - менеджерам при использовании планово-управленческих решений, в значительной мере определяют и всю эффективность систем и методов сетевого моделирования.

При разработке рабочего проекта мероприятий в землеустройстве в реальных условиях создаются, кроме того, документы, отражающие затраты времени, трудовых, материальных и финансовых ресурсов; а иногда – только затрат времени. Параметрами сетевого графика являются временные оценки начала и окончания работ, ранние и поздние сроки свершения событий, продолжительность путей (от исходного до завершающего события), резервы времени, коэффициент напряженности работ. Приведем параметры сетевого графика и математические формулы для их расчета.

		Ранний срок начала первой работы в сетевом графике, от исходного события до события 1.
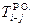		Ранний срок окончания любой работы в сетевом графике от события i до события j; он равен сумме раннего срока начала работы и ее продолжительности.
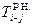		Ранний срок начала любой работы в сетевом графике, от события i до события j, т.е. продолжительность пути от исходного события до момента начала данной работы, Тi-j.
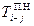		Поздний срок начала любой работы в сетевом графике, от события i до события j; это срок, которые не вызывает задержки свершения завершающего события.
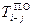		Поздний срок окончания любой работы в сетевом графике, от события i до события j.
	Ri-j	Резерв времени для любой работы i-j в сетевом графике. Это время, на которое можно увеличить продолжительность работы i-j (или перенести срок ее начала), не изменив позднего срока свершения завершающего события сетевого графика. Полный резерв времени для каждой работы определяется как разность между поздним и ранним сроком ее начала (или окончания).
	Ti-j	Продолжительность любой работы в сетевом графике.
	Ti-j (кр)	Продолжительность любой работы на критическом пути сетевого графика. Рассчитанные параметры сетевого графика позволяют организовать эффективное ведение производственных процессов, компенсируя возникающие отклонения путем обоснованного перераспределения ресурсов, сосредотачивая внимание на работах критического пути. У работ и событий, лежащих на критическом пути, запаса по времени нет; т.е. Ri(кр)=0 и Ri-j(кр)=0.