Действия над матрицами
МАТРИЦЫ
2.1. Основные понятия
Напомним, матрицей в математике называется двумерный массив элементов 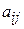 (чисел, функций или иных величин, над которыми можно производить алгебраические операции), расположенных в виде прямоугольной таблицы. Если таблица имеет m строк и n столбцов, то говорят о (m ´ n)-матрице. Обозначения:
(чисел, функций или иных величин, над которыми можно производить алгебраические операции), расположенных в виде прямоугольной таблицы. Если таблица имеет m строк и n столбцов, то говорят о (m ´ n)-матрице. Обозначения:
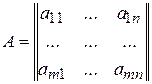 или
или 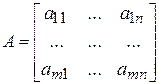 .
.
Одномерный массив называют вектором. Матрица, состоящая из одной строки, называется вектором-строкой, из одного столбца – вектором-столбцом. Если m = n, то матрица квадратная, а число n – ее порядок. Квадратная матрица, у которой лишь диагональные элементы 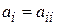 отличны от нуля, называется диагональной и обозначается
отличны от нуля, называется диагональной и обозначается 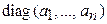 . Если все
. Если все 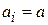 , получают скалярную матрицу. При a = 1 матрица единичная и обозначается I или E. Матрица, все элементы которой равны нулю, называется нулевой.
, получают скалярную матрицу. При a = 1 матрица единичная и обозначается I или E. Матрица, все элементы которой равны нулю, называется нулевой.
Числа и переменные в Matlab рассматриваются как матрицы размера 1 ´ 1 (векторизация). Векторизация обеспечивает упрощение записи операций, производимых одновременно над всеми элементами векторов и матриц, повышение скорости их выполнения. Matlab допускает задание и использование и многомерных массивов.
Для задания матрицы используется команда присваивания. Например, следующими командами формируются матрицы: а) »a = [1 2 1; 4 5 4] – матрица размера 2 ´ 3 с соответствующими элементами; б) »b = [7 8 9] – вектор-строка; в) »c = [2; 2; 3.5] – вектор-столбец; г) »d = zeros(3, 5) – матрица размера 3 ´ 5 с нулевыми элементами. Результаты* приведены в табл. 2.1.
Таблица 2.1
| Матрица размера 2 ´ 3 | Вектор-строка | Вектор-столбец | Матрица размера 3 ´ 5 с нулевыми элементами |
| »a = [1 2 1; 4 5 4] a = 1 2 1 4 5 4 | »b = [7 8 9] b = 7 8 9 | »c = [2; 2; 3.5] c = 2.0000 2.0000 3.5000 | »d = zeros(3, 5) d = 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
Две записи для вектора – b = [l 2 3 4] и b = [1,2,3,4] – идентичны, векторы задаются списком своих элементов, разделяемых пробелами или запятыми.
Массив формируется прямым (построчным) перечислением его элементов (например, a = [1 3 5 7; 4 5 6 7] – 2 строки и 4 столбца, b = [1; 3; 5; 7] – столбец с 4 элементами) или заданием диапазона значений в формате [нач.знач. : шаг : кон.знач.] с указанным или единичным (по умолчанию) шагом – [1:2:7], [4:7], [ [1:2:7]; [4:7] ].
Доступ к элементам или блокам элементов массива производится указанием индексов или массива индексов:
a(2, k) – элемент второй строки и k-го столбца;
a(:, k) – k-й столбец;
a(1:3; 1:4) – подматрица из первых 3 строк и 4 столбцов матрицы;
c(:, :, 12) – 12-я страница трехмерного массива.
Массивы хранятся в памяти по столбцам, поэтому с многомерным массивом можно работать как с одномерным, например: A(:) – вектор-столбец из всех элементов массива А; A(13:17) – столбец из элементов с номерами от 13 до 17. Итак:
• при задании массива значения заключать в квадратные скобки;
• элементы в строке массива разделять пробелами или запятыми;
• при указании списка индексов использовать круглые скобки и разделительные запятые (указание индекса символом «:» соответствует заданию всех значений по соответствующему индексу).
При работе с массивами можно пользоваться списками: 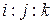 означает «от i до k с шагом j»,
означает «от i до k с шагом j», 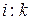 – то же с шагом 1, например,
– то же с шагом 1, например, 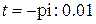 или d = 0 : 8.
или d = 0 : 8.
В Matlab предусмотрен ряд особых функций для задания векторов и матриц, например: а) нулей – zeros(n), zeros(m, n), zeros(m, n, p,…), zeros(size(A)) (соответственно массивы одномерный, двумерный, многомерный и соразмерный с массивом A); б) единиц – ones(n), ones(m, n), ones (size(A)) и др.
Функция magic(n) задает так называемый магический квадрат – матрицу размера 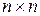 , у которой сумма всех столбцов, всех строк и даже диагоналей равна одному и тому же числу. Пример представлен в табл. 2.2.
, у которой сумма всех столбцов, всех строк и даже диагоналей равна одному и тому же числу. Пример представлен в табл. 2.2.
| Таблица 2.2 | ||||
| Магический квадрат 3 ´ 3 | Сумма по столбцам и строкам | Сумма по диагоналям | ||
| »b = magic(3) b = 8 1 6 3 5 7 4 9 2 | »sum(b) ans = 15 15 15 | »sum(b') ans = 15 15 15 | »sum(diag(b)) ans = | »sum(diag(b')) ans = |
Функция rand генерирует массивы случайных чисел, значения элементов которых равномерно распределены в промежутке (0, 1): rand(n, m) – возвращает матрицу размера n ´ m; rand(n) – квадратную матрицу:
»rand(3) % матрица размера 3´3
ans =
0.9501 0.4860 0.4565
0.2311 0.8913 0.0185
0.6068 0.7621 0.8214
Можно выполнять операции не только с действительными, но и с комплексными числами. Мнимая единица представляется символами i, j*. В табл. 2.3 приведена последовательность действий с комплексными значениями.
Таблица 2.3
| Ввод числа a | Ввод числа b | Произведение двух комплексных чисел | Экспонента от произведения |
| »a = 5 + 2i a = 5.0000 + 2.0000i | »b = 3 – 3i b = 3.0000 – 3.0000i | »с = a*b с = 21.0000 – 9.0000i | »exp(с) ans = –1.2016e+009 – 5.4351e+008i |
Перестановка в матрице строк со столбцами даст транспонированную матрицу A', или AT. Если элементы матрицы комплексно-сопряженные, то это комплексно-сопряженная матрица А. Если элементы транспонированной матрицы A' комплексно-сопряженные, то матрица А* называется сопряженной с А. Определитель квадратной матрицы А обозначается 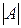 или det A. В табл. 2.4 представлены примеры операций с матрицами.
или det A. В табл. 2.4 представлены примеры операций с матрицами.
Таблица 2.4
| Ввод матрицы A | Ввод матрицы B | Транспони- рование A | Определи- тель B | Собственные числа матрицы B |
| »A = [5 6 4;7 10 5] A = 5 6 4 7 10 5 | »B = [5 6 4;7 10 5; 3 6 9] B = 5 6 4 7 10 5 3 6 9 | »A' ans = 5 7 6 10 4 5 | »det(B) ans = | »eig(B) ans = 18.7965 0.7104 4.4931 |
Некоторые типы матриц естественно возникают при решении разных задач [4], имеют специальные названия и соответствуют некоторому определяющему условию: 1) симметричная – 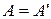 , 2) кососимметричная –
, 2) кососимметричная – 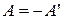 , 3) ортогональная –
, 3) ортогональная – 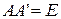 , или
, или 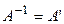 , 4) стохастическая –
, 4) стохастическая – 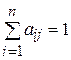 для
для 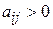 , 5) эрмитова –
, 5) эрмитова – 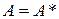 , 6) унитарная –
, 6) унитарная – 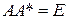 , или
, или 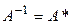 .
.
Не менее важны специальные типы матриц, используемые в качестве вспомогательных (тестовые матрицы, матрицы Адамара, Гильберта и др.). Приведем некоторые из них:
1) Н = hadamard(n) – формирует матрицу Адамара порядка n. Матрица Адамара – это квадратная матрица размера n, составленная из двух значений 1 и –1, столбцы которой ортогональны, так что справедливо соотношение Н'*Н = n*I, где I =eye(n, n) – единичная квадратная матрица размера n ´ n:
»H2 = hadamard(2)
H2 =
1 1
1 –1
Матрицы Адамара применяются в различных областях, включая комбинаторику, численный анализ, обработку сигналов. Матрица Адамара размера n ´ n при n >2 существует, если n делится на 4 без остатка. Алгоритм Matlab вносит дополнительные ограничения, вычисляя матрицы Адамара только для тех n, когда или n, или n/12, или n/20 являются степенями по основанию 2.
2)hilb(n) – возвращает матрицу Гильберта порядка n. Матрица Гильберта является примером плохо обусловленной матрицы. Элементы матрицы Гильберта определяются как H(i, j)=l/(i + j –1).
Таблица 2.5
| Матрица Гильберта | Инверсная матрица | Произведение прямой и инверсной матриц |
| »H = hilb(2) H = 1.0000 0.5000 0.5000 0.3333 | »H1 = invhilb(2) H1 = 4 –6 –6 12 | »H * H1 ans = 1 0 0 1 |
3)invhilb(n) – возвращает матрицу, обратную матрице Гильберта порядка n (n <15). Для n >15 функция invhilb(n) возвращает приближенную матрицу. Получение матриц представлено в табл. 2.5. Точная обратная матрица – это матрица с очень большими целочисленными значениями, которые могут быть представлены как числа с плавающей запятой без погрешности округления до тех пор, пока порядок матрицы n не превышает 15.
Формирование матриц
1. Объединение матриц в одну. Часто удобно использовать матрицы, состоящие из блоков, при этом блоки являются матрицами меньших размеров. При умножении такой блочной матрицы на число, нужно умножить все ее блоки на это число. При надлежащем согласовании разбиений действия сложения и умножения блочных матриц осуществляются так, как будто вместо блоков стоят числа.
Существуют различные способы создания такой матрицы.
Первый способ. Объединение массивов «по горизонтали» (одинаковое число строк) – [A, B, C] или [A B C] и «по вертикали» (одинаковое число столбцов) – [A; B; C]. Обеспечивается операция «конкатенация».
Таблица 2.6
| Единичная матрица | Матрица нулей | Матрица c |
| »a = eye(2) a = 1 0 0 1 | »b = zeros(2) b = 0 0 0 0 | »c = [0 1; 1 0] c = 0 1 1 0 |
Пусть сформированы матрицы, представленные в табл. 2.6. На их основе можно построить матрицу, содержащую 4 матрицы:
»CNOT = [a b; b c]
CNOT =
1 0 0 0
0 1 0 0
0 0 0 1
0 0 1 0
Второй способ. Команда С=cat(dim, А, В) – объединяет массивы А и B в соответствии со спецификацией размерности dim и возвращает объединенный массив (табл. 2.7): dim=1 – вертикальная конкатенация, dim=2 – горизонтальная, dim=3 – многомерный массив размерности 3 и т. д.
Таблица 2.7
| Вертикальная конкатенация | Горизонтальная конкатенация | |
| »CNOT1 = cat(1, a, b) | »CNOT2 = cat(1, b, c) | »CNOT = cat(2, CNOT1, CNOT2) |
| CNOT1 = 1 0 0 1 0 0 0 0 | CNOT2 = 0 0 0 0 0 1 1 0 | CNOT = 1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 |
Таблица 2.8
| Исходная матрица | Копирование матрицы | Выборка по столбцам |
| »w = [1 0 2;6 5 2] | »t = repmat (w, 2, 2) | »s = reshape(w, 3, 2) |
| w = 1 0 2 6 5 2 | t = 1 0 2 1 0 2 6 5 2 6 5 2 1 0 2 1 0 2 6 5 2 6 5 2 | s = 1 5 6 2 0 2 |
Третий способ. Для создания матриц, состоящих из других матриц, используются функции: repmat(А, m, n) – возвращает матрицу B, состоящую из m ´ n копий матрицы A, т. е. в матрице m ´ n каждый элемент заменяется на копию матрицы A; reshape(А, m, n) – возвращает матрицу B размера m ´ n, сформированную из А последовательной выборкой по столбцам. Если число элементов А не равно m ´ n, то выдается сообщение об ошибке.
Варианты реализации команд третьим способом приведены в табл. 2.8.
2. Перестановки элементов матриц. Для перестановок элементов матриц служат следующие функции:
1) B = fliplr(A) – зеркально переставляет столбцы матрицы А относительно вертикальной оси; 2) B = flipud(A) – зеркально переставляет строки матрицы А относительно горизонтальной оси; 3) P = perms(v) – возвращает матрицу P, которая содержит все возможные перестановки элементов вектора v, каждая перестановка в отдельной строке. Матрица Р содержит n! строк и n столбцов; 4) rot90(A, n) – поворот матрицы А на 90°*n. Варианты выполнения перестановок элементов матриц представлены в табл. 2.9.
Таблица 2.9
| Зеркальная перестановка столбцов | Зеркальная перестановка строк | Поворот матрицы | |||
| »F = [1 2 3;5 45 3] F = 1 2 3 5 45 3 | »fliplr(F) ans = 3 2 1 3 45 5 »flipud(F) ans = 5 45 3 1 2 3 | »F1 = [1 2 3] F1 = 1 2 3 | »perms(F1) ans = 3 2 1 3 1 2 2 3 1 2 1 3 1 2 3 1 3 2 | »a a = 1 0 0 1 | »rot90(a, 3) ans = 0 1 1 0 |
3. Изменение размеров массива. Для удаления отдельных столбцов и строк матрицы используются пустые квадратные скобки [ ]. Примеры удалений приведены в табл. 2.10.
Таблица 2.10
| Матрица | Удаление второго столбца | Удаление первой строки |
| »M = [1 2 3; 4 5 6; 7 8 9] M = 1 2 3 4 5 6 7 8 9 | »M(:, 2) = [ ] M = 1 3 4 6 7 9 | »M(1, :) = [ ] M = 4 6 7 9 |
Таблица 2.11
| Удаление одинаковых элементов вектора | Объединение множеств | Пересечение множеств | Разность множеств |
| »f = [1 1 3 4 4 5 6] f = 1 1 3 4 4 5 6 »unique(f) ans = 1 3 4 5 6 | »f = [2 3] f = 2 3 »d = [4 5 6] d = 4 5 6 »union(f, d) ans = 2 3 4 5 6 | »f = [4 3] f = 4 3 »d = [4 5 6] d = 4 5 6 »intersect(d, f) ans = | »f = [4 3] f = 4 3 »d = [4 5 6] d = 4 5 6 »setdiff(d, f) ans = 5 6 |
Имеется возможность объединениямножеств – union(X, Y), пересечения– intersect(X, Y), разности – setdiff(X, Y). Можно также удалить одинаковые элементы вектора функцией unique(X). Примеры приведены в табл. 2.11.
Действия над матрицами
Произведением прямоугольной (m ´ n)-матрицы А на число a называют матрицу, элементы которой получены умножением элементов 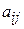 на число a:
на число a:
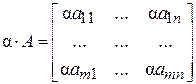 .
.
Сумма определяется для прямоугольных матриц одинакового строения, и элементы суммы равны суммам соответствующих слагаемых, т. е.
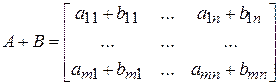
Умножение определяется только для таких прямоугольных матриц, у которых число столбцов первого множителя равно числу строк второго. Произведением (m ´р)-матрицы А на (р ´ n)-матрицу В будет (m ´ n)-матрица С с элементами: 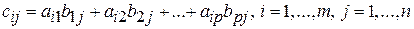 .
.
Матрицы А и В называются перестановочными, если AB = BA. Определитель произведения двух квадратных матриц равен произведению определителей перемножаемых матриц.
Для различения операций (табл. 2.12) над матрицами по правилам линейной алгебры и поэлементных операций с массивами перед знаком операции ставят точку. Примеры использования операций с возможными особенностями их выполнения представлены в табл. 2.13.
Таблица 2.12
| Операции с матрицами | Операции с элементами матриц |
| + сложение | + сложение |
| – вычитание | – вычитание |
| * умножение | .* умножение |
| ^ возведение в степень | .^ возведение в степень |
| / правое деление | ./ правое деление |
| \ левое деление | .\ левое деление |
| ' транспонирование | |
| kron тензорное произведение |
Таблица 2.13
| Ввод матрицы a: | Ввод матрицы b: | Свойства определителя: | |||
| »a = [1 2 3;2 3 1;3 1 2] a = 1 2 3 2 3 1 3 1 2 | »b = [4 5 6;5 6 4;6 4 3] b = 4 5 6 5 6 4 6 4 3 | »det(a)*det(b) ans = | »det(a*b) ans = | ||
| Умножение на число: | Сумма матриц: | Произведение матриц: | |||
| »6.*a ans = 6 12 18 12 18 6 18 6 12 | »a+b ans = 5 7 9 7 9 5 9 5 5 | »a*b ans = 32 29 23 29 32 27 29 29 28 | |||
| Ввод матрицы c: | Ввод матрицы d: | Различают правое (справа налево) и левое деление: | |||
| »c = [1 1 1;2 2 2;3 3 3] c = 1 1 1 2 2 2 3 3 3 | »d = [4 4 4;5 5 5;6 6 6] d = 4 4 4 5 5 5 6 6 6 | »c.\d ans = 4.0000 4.0000 4.0000 2.5000 2.5000 2.5000 2.0000 2.0000 2.0000 »c./d ans = 0.2500 0.2500 0.2500 0.4000 0.4000 0.4000 0.5000 0.5000 0.5000 | |||
| Возведение в степень: | |||||
| »c.^2 % поэлементное ans = 1 1 1 4 4 4 9 9 9 | »c^2 ans = 6 6 6 12 12 12 18 18 18 | »c^0 ans = 1 0 0 0 1 0 0 0 1 | |||
Система Matlab в режиме прямых вычислений над векторами и матрицами наряду с обычными арифметическими и алгебраическими действиями выполняет такие операции, как инвертирование матрицы, вычисление ее собственных значений и векторов, решение систем линейных уравнений, вывод графиков двумерных и трехмерных функций и многое другое.
Матрица 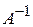 называется обратной к квадратной матрице А, если A
называется обратной к квадратной матрице А, если A 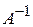 = E, при этом
= E, при этом 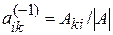 . Невырожденность матрицы А есть необходимое и достаточное условие существования обратной матрицы, которая при этом оказывается единственной и перестановочной с исходной. Квадратная матрица А =(
. Невырожденность матрицы А есть необходимое и достаточное условие существования обратной матрицы, которая при этом оказывается единственной и перестановочной с исходной. Квадратная матрица А =( 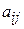 ) называется невырожденной, если ее определитель не равен нулю; в противном случае матрица называется вырожденной (особенной).
) называется невырожденной, если ее определитель не равен нулю; в противном случае матрица называется вырожденной (особенной).
Таблица 2.14
| Ввод матрицы | Определитель | Обратная матрица | Проверка 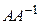 =E =E |
| »A = [4 6 7; 11 1 9; 2 2 2] A = 4 6 7 11 1 9 2 2 2 | »det(A) ans = | »inv(A) ans = –0.3077 0.0385 0.9038 –0.0769 –0.1154 0.7885 0.3846 0.0769 –1.1923 | »A*inv(A) ans = 1.0000 –0.0000 0 –0.0000 1.0000 0 0 –0.0000 1.0000 |
| »B = [5 6 4; 7 10 5; 3 6 9] B = 5 6 4 7 10 5 3 6 9 | »det(B) ans = | »inv(B) ans = 1.0000 –0.5000 –0.1667 –0.8000 0.5500 0.0500 0.2000 –0.2000 0.1333 | »B*inv(B) ans = 1.0000 0.0000 –0.0000 –0.0000 1.0000 –0.0000 0 0.0000 1.0000 |
| »inv(B*A) ans = –0.1577 –0.0058 0.1737 0.1731 –0.1827 0.1122 0.0846 0.0885 –0.2192 | »inv(A)*inv(B) ans = –0.1577 –0.0058 0.1737 0.1731 –0.1827 0.1122 0.0846 0.0885 –0.2192 |
Примеры применения дополнительных операций над матрицами показаны в табл. 2.14. Верна формула 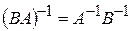 .
.
