Составные высказывания
С помощью рассмотренных в предыдущем пункте логических операций из заданной совокупности атомов (элементарных высказываний) можно строить различимо составные высказывания. Порядок выполнения действий указывается скобками.
Истинностное значение составного высказывания зависит только от истинностных значений образующих его атомов, оно может быть найдено на основании определение логических операций с помощью таблиц истинности.
Пример. 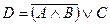 .
.
| A | B | C | 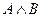 | 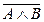 | 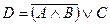 |
| И | И | И | И | Л | И |
| И | И | Л | И | Л | Л |
| И | Л | И | Л | И | И |
| И | Л | Л | Л | И | И |
| Л | И | И | Л | И | И |
| Л | И | Л | Л | И | И |
| Л | Л | И | Л | И | И |
| Л | Л | Л | Л | И | И |
Основные логические операции. Формулы логики.
Логические операции.
Пусть A, В - произвольные высказывания, относительно которых не предполагается, что известно их истинностные значения.
Связке "НЕ" соответствует логическая операция отрицания, обозначение операции – знак ù или  .
.
Определение. Отрицанием высказывания A называется высказывание 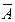 (ùA), которое истинно, если A – ложно, и ложно, если A – истинно.
(ùA), которое истинно, если A – ложно, и ложно, если A – истинно.
Таблица истинности отрицания:
| A | 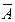 |
| И | Л |
| Л | И |
Пример: A: 2*2=4 – истинное высказывание; 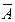 :
: 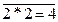 или 2*2
или 2*2 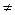 4 - ложное высказывание.
4 - ложное высказывание.
Связке "И" соответствует операция конъюнкция, обозначение операции – знак 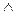 (или &).
(или &).
Определение. Конъюнкцией высказываний A и B называется высказывание A 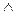 B (читается "A и B"), которое истинно тогда и только тогда, когда A, B – истинно.
B (читается "A и B"), которое истинно тогда и только тогда, когда A, B – истинно.
Таблица истинности конъюнкции:
| A | B | A 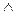 B B |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | Л |
Пример: A: 5 – нечетное число; B: Пушкин родился в 1799 г – истинные высказывания; поэтому высказываниеA 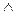 B: 5 – нечетное число
B: 5 – нечетное число 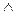 Пушкин родился в 1799 г. – истинное высказывание.
Пушкин родился в 1799 г. – истинное высказывание.
Связке "ИЛИ" соответствует операция дизъюнкция, обозначение операции – знак 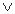 .
.
В формально-логических выводах «или» употребляется не в исключающем смысле (в отличие от обыденной речи, где эта связка может употребляться и в исключающем смысле и в неисключающем смысле)
Определение. Дизъюнкцией высказываний A и B называется высказывание A 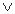 B (читается "A или B"), которое ложно тогда и только тогда, когда A, B – ложны.
B (читается "A или B"), которое ложно тогда и только тогда, когда A, B – ложны.
Таблица истинности дизъюнкции:
| A | B | A 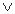 B B |
| И | И | И |
| И | Л | И |
| Л | И | И |
| Л | Л | Л |
Пример. A: 7<10, и.в. В: 3 - число четное, л.в. A 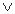 B: 7<10
B: 7<10 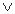 3 - число четное, и.в.
3 - число четное, и.в.
Связке "ЕСЛИ....ТО" соответствует логическая операция импликация, обозначение операции знак →.
Определение. Импликацией высказываний A и B называется высказывание A→B (читается "если A, то B"), которое ложно тогда и только тогда, когда A – истинно, а B – ложно.
Таблица истинности импликации:
| A | B | A→B |
| И | И | И |
| И | Л | Л |
| Л | И | И |
| Л | Л | И |
Пример. A: 2*2=5, л. в. В: 2=2, и. в. A→B: 2*2=5→ 2=2. и. в.
Высказывание A называется условием или посылкой, высказывание В - заключением или следствием импликации.
Связке "ТОГДА И ТОЛЬКО ТОГДА, КОГДА" соответствует операция эквиваленция, обозначение операция – знак «.
Определение. Эквиваленцией высказываний A и В навивается высказывание, обозначаемое A«B (читается :"A тогда и только тогда, когда В" или короче: "A эквивалентно В"), которое считается истинным только тогда, когда оба высказывания A и В имеют одинаковое истинностное значение.
Эквивалентность А«В читается также следующим образом: "Для того, чтобы A, необходимо и достаточно, чтобы В".
Таблица истинности эквиваленции:
| A | B | A«B |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | И |
Пример. A: 7 – число простое; и.в. В: в равнобедренном треугольнике при основании углы равны, и.в. A«В - и.в.
1) Стрелка Пирса - ↓.
Логическая операция задается таблицей:
| р | q | р ↓ q |
Стрелка Пирса является отрицанием дизъюнкции.
2) Штрих Шеффера - |.
Логическая операция задается таблицей:
| р | q | р | q |
Штрих Шеффера является отрицанием конъюнкции.
3) Сумма по модулю два - 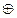
Логическая операция задается таблицей:
| р | q | р 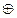 q q |
Сумма по модулю два является отрицанием эквивалентности
