Интегральный признак Коши

Теорема: Если каждый член положительного ряда меньше предшествующего, то: а) если предел 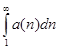конечный, то ряд (1) сходится, б) если предел бесконечный, то ряд (1) расходится.

@ Задача 5. Исследовать на сходимость гармонический ряд .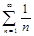

Решение: Из интегрального признака Коши 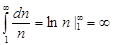следует, что ряд расходится.

Ряд называется знакопеременным, если его члены поочередно положительны и отрицательны. Достаточным признаком сходимости знакопеременного числового ряда являются признак Лейбница.

Признак Лейбница

Знакопеременный ряд сходится, если его члены стремятся к нулю, все время убывая по абсолютному значению.

! Пример: Знакопеременный ряд 1 – 1/2 + 1/3 – 1/4 + ··· сходится согласно признаку Лейбница.

Знакопеременный ряд называется абсолютно сходящимся, если сходится положительный ряд, составленный из абсолютных значений членов данного ряда.

! Пример: Знакопеременный ряд 1 – 1/4 + 1/9 – 1/16 + ··· является абсолютно сходящимся.

Знакопеременный рядможет сходиться и тогда, когда ряд, составленный из абсолютных значений его членов, расходится.

Знакопеременный ряд называется условно сходящимся, если он сходится, но ряд, составленный из абсолютных значений его членов, расходится.

! Пример: Знакопеременный ряд 1 – 1/2 + 1/3 – 1/4 + ··· является условно сходящимся.

СТЕПЕННЫЕ РЯДЫ

Ряд, членами которого являются степенные функции, называется степенной

,

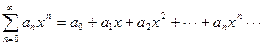где числа а₀, а₁, ¼ а_п называются коэффициентами ряда.

При x = x₀ степенной ряд превращается в числовой ряд. Если полученный числовой ряд сходится, то точка x₀ называется точкой сходимости ряда, если ряд расходится – точкой расходимости.

Совокупность числовых значений x, при которых степенной ряд сходится, называется его областью сходимости.

Теорема Абеля

Если степенной ряд сходится при x = x₀ ¹ 0, то он абсолютно сходится при всех значениях |x| < |x₀|.

Следствие: Если ряд расходится при x = x₁, тоон расходится и при всех |x| > |x₁|.

Из теоремы Абеля следует, что если x₀ ¹ 0 есть точка сходимости степенного ряда, то интервал (– |x₀|;|x₀|)весь состоит из точек сходимости данного ряда; при всех значениях x вне этого интервала степенной ряд расходится.

Интервал (– |x₀|;|x₀|)называется интервалом сходимости степенного ряда. Число R = |x₀|называется радиусом сходимости степенного ряда, т.е. при всех x, для которых |x| < R, ряд абсолютно сходится, а при |x| > R ряд расходится.

В частности, когда степенной ряд сходится лишь в одной точке x₀ = 0, то считается, что R = 0. Если же ряд сходится при всех значениях x Î R (т.е. во всех точках числовой оси), то считается, что R = ∞.

Отметим, что на концах интервала сходимости (т.е. при x = R и при x = – R) сходимость ряда проверяется в каждом конкретном случае отдельно.

Согласно признаку Даламбера радиус сходимости степенного ряда определяется как 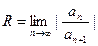, а согласно признаку Коши - R = 1/.

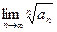@ Задача 1. Найти радиус сходимости степенного ряда .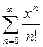

Решение: Радиус сходимости можно найти по формуле Даламбера

= .

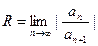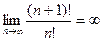Следовательно, степенной ряд абсолютно сходится на всей числовой оси.

@ Задача 2. Найти радиус сходимости степенного ряда .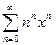

Решение: Радиус сходимости находим по формуле Коши

R = 1/= .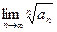

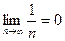Следовательно, степенной ряд сходится лишь в одной точке x₀ = 0.