Интегральный признак Коши. Пусть для функции f(x) выполняется:

Пусть для функции f(x) выполняется:

1. 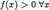(функция принимает только положительные значения)

2. 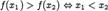(функция монотонно убывает)

3.

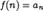
Тогда ряд 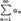и несобственный интеграл 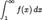сходятся или расходятся

Знакопеременные ряды. Абсолютная и условная сходимость.

Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным. Частным случаем знакопеременного ряда является знакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки.

Признак Лейбница

Для знакочередующихся рядом действует достаточный признак сходимости Лейбница.

Пусть {a_n} является числовой последовательностью, такой, что

1. a_n+1 < a_n для всех n;

2.

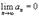
Тогда знакочередующиеся ряды 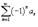и 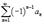сходятся.

Абсолютная и условная сходимость

Ряд 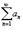называется абсолютно сходящимся, если ряд 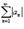также сходится. Если ряд 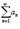сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.

Ряд 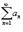называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

Знакочередующиеся ряды. Признак Лейбница.

Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.: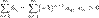

Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы: Пусть для знакочередующегося ряда 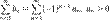выполняются следующие условия:

1. 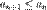(монотонное невозрастание {an}

2. 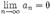Тогда этот ряд сходится.

Степенные ряды. Теорема Абеля. Радиус сходимости.

Определение 1. Степенным рядом называется функциональный ряд вида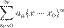

,где a_n - коэффициенты степенного ряда, x_0 - центр ряда.

Теорема 1: Теорема Абеля.

Пусть ряд 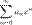сходится в точке x. Тогда он сходится при любом x, удовлетворяющем неравенству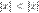

, причём на любом отрезке внутри интервала 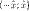сходимость равномерная.

Следствие из теоремы Абеля.

Если ряд 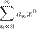расходится в точке x, то он расходится и при любых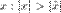

Теорема 2: Теорема о радиусе сходимости.

Для каждого степенного ряда 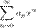существует 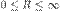, удовлетворяющее свойствам:

1. Если R=0, то ряд сходится только при x=0

2. Если R=беск, то ряд сходится при любых x(-беск.: беск)

3. Если 0<R<беск, то ряд сходится при (-R:R) и расходится при x не пренад (-R:R)

Формула Тейлора, ряд Тейлорв.

Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.

Пусть функция f(x) бесконечно дифференцируема в некоторой окрестности точки a. Формальный ряд 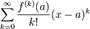называется рядом Тейлора функции f в точке a.