Основное свойство колец без делителей нуля
Пусть К – кольцо без делителей нуля и a≠0, тогда из равенства ab=ac следует, что b=c.
Доказательство.
Из равенстваab=ac следует, что a(b—c)=0. Так как элемент а ненулевой, то b–c=0, т.е. b=c.
□
Обратим внимание, что данное свойство означает логическое сокращение, а не умножение на элемент, обратный к элементу «а». Кстати, такого обратного может и не существовать.
Деление с остатком.
Помните фильм про Буратино и знаменитый диалог Лисы Алисы и Кота Базилио: “Пять на два не делится! Вот тебе, Базилио, один золотой, а вторую неделящуюся половину я забираю себе!” Кот ничего не понял, но почувствовал, что его обманывают.
Что означает «делится», мы выше видели, это когда есть дополнительный множитель и он восстанавливает равенство. А если множителя нет. Тут мы вступаем на зыбкую почву приближений.
При делении целых чисел и многочленов разные числа и многочлены можно легко сравнивать. У чисел сравнение ведется путем сравнения их модулей, а у многочленов – сравнением их степеней. Поэтому при неполном делении стремятся, что бы степень остатка была меньше, чем степень делителя.
Формально понятие степени можно ввести так.
Определение. Пусть К – кольцо без делителей нуля. Степенью элементов кольца К называется отображение 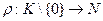 ненулевых элементов кольца во множество натуральных чисел такое, что выполняется условие монотонности:
ненулевых элементов кольца во множество натуральных чисел такое, что выполняется условие монотонности: 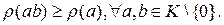 Другими словами, степень произведения не меньше степени сомножителя. (Обратим внимание, что для нуля степень не определена!)
Другими словами, степень произведения не меньше степени сомножителя. (Обратим внимание, что для нуля степень не определена!)
Если определено понятие степени элемента, то можно говорить о делении с остатком.
Определение Кольцо К называется кольцом с алгоритмом деления с остатком или евклидовым, если 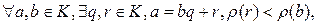 или r=0.
или r=0.
Евклидовых колец не очень много. Нас же будут в основном интересовать два из них.
Пример 1.
Кольцо целых чисел Z является евклидовым, при этом степенью целого числа является его модуль. Алгоритм деления с остатком в кольце целых чисел изучался в школе.
Пример 2.
Пусть P – поле, тогда кольцо многочленов P[x] является евклидовым, при этом степенью является обычная степень многочлена. Алгоритм деления с остатком – обычное деление многочленов уголком.
Сейчас мы докажем самую полезную теорему о евклидовых кольцах, которая применяется чуть не всей классической алгебре и криптографии.
Но прежде введем понятие наибольшего общего делителя (НОД) и двойственное ему наименьше обще кранное (НОК).
Определение. Элемент d=НОД(a,b) называется наибольшим общим делителем элементов a и b, если выполняются два условия:
1) d\a, d\b – т.е. d - общий делить,
2) Если s\a, s\b , то s\d – наибольший делитель, в том смысле, что он делится на все остальные делители.
Понятие наименьшего общего кратного НОК не так важно как НОД, но его введение поучительно в силу свой двойственности к НОД. «Наибольший» заменяется на «наименьший», «делится» на «делит».
Определение. Элемент m=НОК(a,b) называется наименьшим общим кратным элементов a и b, если выполняются два условия:
1) m: a\m, b\m - общий кратный,
2) Если a\n, b\n , то m\n – наименьшее кратное, в том смысле, что оно делит все остальные кратные.
Фундаментальный факт состоит в том, что в евклидовых кольцах, а значит в кольце целых чисел и кольце многочленов над полем, – НОД существует и его можно выразить через исходные элементы.
