Геометрическая интерпретация конъюнкций и дизъюнкций
Рассмотрим произвольные булевы ф-ции f1 и f2 , которым соответсвуют множества единиц Nf1 и Nf2, тогда конъюнкции ф-ций f1, f2 будет соответствовать пересечение соответствующих множеств: f1 Ù f2 « Nf1 Ç Nf2 .
Действительно, единицы конъюнкции есть в точности те наборы, на которых обе ф-ции f1 и f2 равны 1. А это есть пересечение множеств Nf1 и Nf2 , т.е. те наборы, которые принадлежат и Nf1 , и Nf2 .
Дизъюнкция f1Ú f2 « Nf1 È Nf2 (объединение).
Действительно, единицы дизъюнкции есть наборы, на которых или f1= 1 или f2= 1. Это и есть объединение множеств Nf1 и Nf2.
Определение:Интервалом называют множество единиц некоторой элементарной конъюнкции.
Например: Интервал N (x1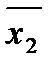 
) - есть те вершины булева куба, на которых данная конъюнкция равна 1, т. е. x1 = 1,
x2 = 0, т. е. для трехмерного булева куба это вершины 101 и 100 (ребро).
Интервал, соответствующий конъюнкции x1, есть наборы, в которых x1 = 1
111 — это есть квадрат
Утверждение: Если удалить множитель из элементарной конъюнкции, то полученной конъюнкции будет соответствовать интервал, который содержит начальный.
Действительно:
Пусть начальный интервал соответствует конъюнкции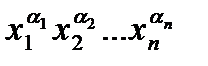 
. Удаляя первый множитель из данной конъюнкции, получим интервал, соответствующий конъюнкции 
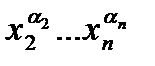. Интервал, соответствующий начальной конъюнкции, есть множество наборов, удовлетворяющих следующим соотношениям 
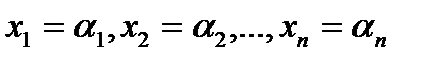. Полученный интервал есть множество наборов, удовлетворяющих следующим условиям 
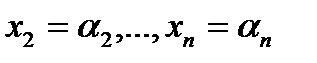, которое содержит начальное.
Определение:Рангом интервала называют ранг соответствующей конъюнкции.
Определение:Размерностью интервала называют число
(n - rang), т.е. число переменных,которые не вошли в данную конъюнкцию.
Пример: размерность x1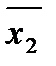 
в трехмерном кубе равна 1. Размерность интервала x1 в трехмерном кубе равна 2.
Определение: Допустимым интервалом для функции f называют интервал, который состоит только из единиц функции f.
Пример: Рассмотрим функцию от трех переменных (рисунок справа), тогда интервал x1 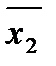является допустимым для данной функции, т.к. он состоит целиком из единиц функции f. Интервал 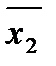x3 допустимым не является, т.к. он содержит 0 функции f, а именно набор 001, на этом наборе значение функции равно 0, а конъюнкция равна 1. Для данной функции 11 допустимых интервалов.
Определение: Максимальным допустимым интервалом называют интервал, при удалении любого множителя из конъюнкции которого получается интервал недопустимый.
Максимальным интервалом является x2 x3 , данный интервал является допустимым, он состоит целиком из 1. Любой интервал, который получается из данного удалением некоторого множителя, будет недопустимым. Интервал x1 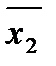максимальным не является, удалим множитель x2 и получим интервал x1, он является допустимым (это передняя боковая грань).
Эквивалентные определения:Допустимый интервал называется максимальным, если он не содержится ни в каком другом допустимом интервале.
Д/з.
Определение:Покрытием единиц булевой функции f называют набор допустимых интервалов, таких что каждая единица булевой функции принадлежит некоторому из интервалов.
Пример:
001 011
x2x3
101 111
x1x2
000 010 x1x2
100 110
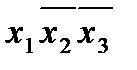
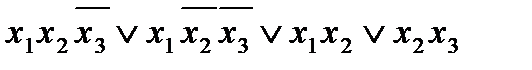
Рассмотрим четыре допустимых интервала, это есть покрытие. Действительно, каждый из интервалов является допустимым, каждый из интервалов состоит целиком из единиц функции f, и каждая единица функции f принадлежит некоторому интервалу (покрыта некоторым интервалом).
Утверждение: Каждое покрытие представляет булеву ф-цию.
Действительно, в силу того, что каждый интервал покрытия является допустимым, на нулевом наборе булевой функции значение каждой конъюнкции интервала равно 0. Если же рассматриваем единичный набор булевой функции (набор, на котором значение функции равно 1), то значение ДНФ, которая соответствует покрытию равна 1, т.к. значение конъюнкции, соответствующей набору, который покрывает данный набор равно 1.
ДНФ, которая соответствует покрытию, представляет булеву функцию.
Утверждение: Любой ДНФ, которая представляет f, соответствует покрытие.
Д/з.
Определение:Тупиковым покрытием называют покрытие, при удалении любого интервала из которого, оно перестает быть покрытием.
Пример: Рассмотренное в предыдущем примере покрытие является тупиковым. Действительно, если удалим интервал x2 x3 , то вершина 011 не будет принадлежать ни одному из оставшихся интервалов. Если удалим x1 x3, то тогда не будет покрыта вершина 101, если удалим x1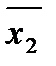 
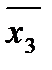, то не будет покрыта вершина 100, если удалим x1 x2 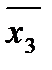, то не будет покрыта вершина 110. Добавим к рассмотренномупокрытию x1 x2, тогда имеем не тупиковое покрытие. Действительно, можно удалить интервал x1 x2 и все равно получим покрытие.