Урок № 83. Тема 9.8.: Решение задач

План занятия.

Определение цилиндра, его элементы, сечения.

Определение конуса, его элементы, сечения.

Задача. Диагональ осевого сечения цилиндра равна 12см и наклонена к плоскости основания под углом 60⁰. Найти Sб., Sполн. цилиндра. Ответ ;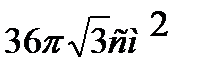

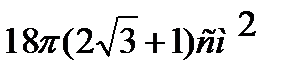
Задача. Радиусы оснований усеченного конуса 8см и 4см, образующая наклонена к плоскости основания под углом 60⁰. Найти Sбок. и S осевого сечения.

Ответ Sб.=96πсм². Sсеч.=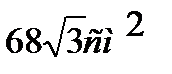

Контрольные вопросы:

1. Определение шара

2. В чем отличие шара от сферы?

3. Формула нахождения площади поверхности шара, сферы.

Тема 10.1.: Объем призмы.

План занятия.

1. Общие представления об объеме.

2. Основные свойства объема.

1. Каждая фигура имеет определенный объем, выраженный неотрицательным числом.

2. Равные фигуры имеют равные объемы.

3. Если фигура разбита на несколько частей, не имеющих общих точек, то ее объем равен сумме объемов частей.

Объем величина, такая как длина отрезка, площадь, величина угла. Объем можно измерить с помощью выбранной единицы измерения объемов. Единицы объема: кубический см (см³) – объем единичного куба с ребром в 1см; аналогично кубический дециметр (дм³); кубическим метр (м³).

Теорема. Объем прямоугольного параллелепипеда равен произведению трех его измерений. V=авс

Теорема. Объем призмы равен произведению площади основания на высоту.

Vпризмы = Sосн.h

Решение задачи

Задача №1. В правильной четырехугольной призме диагональ равна 12см и составляет с плоскостью основания угол 45⁰. Определить объем. Ответ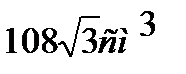

Задача №2. В правильной шестиугольной призме сторона основания равна 4см, а диагональ боковой грани составляет с плоскостью основания угол 60⁰. Определить объем.

Ответ 288см³.

Домашнее задание

1) Конспект.

Задача №1. Объем куба 8м³. Найти Sполн. Ответ 24м².

Задача №2. В правильной треугольной призме сторона основания 6см, а диагональ боковой грани составляет с плоскостью основания угол 30⁰. Определить объем.

Ответ 18см³.

Задача №3. Измерения прямоугольного параллелепипеда 15м, 50м, 36м. Найти ребро равновеликого ему куба. Ответ 26м.

Тема 10.2: Объем пирамиды, объем усеченной пирамиды.

План занятия.

1.Дать определение формулы объема пирамиды

V=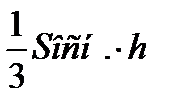

2.Показать модели различных усеченных пирамид и написать формулу объема усеченной пирамиды.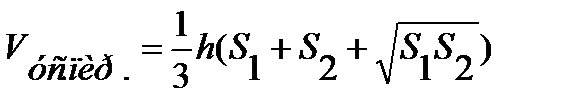

где h – высота усеченной пирамиды.

S₁ – площадь нижнего основания.

S₂ – площадь верхнего основания.

Задача №1. Сторона основания правильной треугольной пирамиды 6см, а боковое ребро образует с плоскостью основания угол 45⁰. Определить объем призмы.

Ответ V=18см³.

Задача №2. Основание пирамиды служит прямоугольник со сторонами 9м и 12м. Каждое из боковых ребер равно 12,5м. Найти объем. Ответ 360м³.

Задача №3. Высота усеченной пирамиды равна 15м, объем равен 475м³. Площади оснований относятся как 4:9. Определить площади этих оснований. (20м², 45м²)

Задача №4. В правильной четырехугольной усеченной пирамиде V=430м³ h=10м. Сторона одного основания 8м. Определить сторону другого основания. (5м).

Задача №3. Определить объем правильной шестиугольной усеченной пирамиды, если стороны оснований а и в, а боковое ребро составляет с плоскостью нижнего основания угол 30⁰.

V=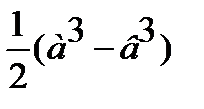

Домашнее задание.

1) Выучить конспект.

Задача №1. В правильной четырехугольной пирамиде высота 3м, боковое ребро 5м. Найти объем. Ответ V=32м³.

Задача №2. Апофема треугольной правильной пирамиды равна 10м. Высота 8м. Определить объем. Ответ V=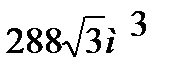

Задача. Боковое ребро правильной четырехугольной усеченной пирамиды равно 3м, стороны оснований 5м и 1м. Определить объем.