Функции двух переменных
Приращение функции

Функция, дифференцируемая в точке 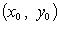
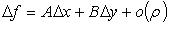 при
при 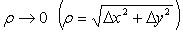
В этом случае дифференциал функции в точке  :
:
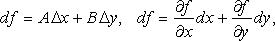
 - частные производные, вычисленные в точке
- частные производные, вычисленные в точке  .
.
Дифференцирование композиции
1. Если 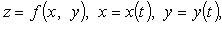 то
то
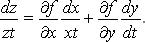
2. Если 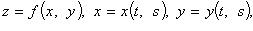 то:
то:
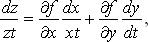
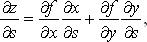
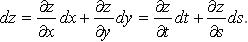
Однородная функция степени k
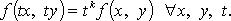
3. Пределы и непрерывность
Исследование пределов и непрерывности в многомерных пространствах приводит ко многим нелогичным и патологическим результатам, не свойственным функциям одной переменной. Например, существуют скалярные функции двух переменных, имеющих точки в области определения, которые при приближении вдоль произвольной прямой дают специфический предел, и дают другой предел при приближении вдоль параболы. Функция
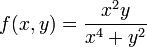
стремится к нулю по любой прямой, проходящей через начало координат. Однако, когда к началу координат приближаются вдоль параболы 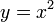 , предел = 0.5. Так как пределы по разным траекториям не совпадают, предела не существует.
, предел = 0.5. Так как пределы по разным траекториям не совпадают, предела не существует.
Функция 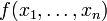 имеет пределом число A при стремлении переменных
имеет пределом число A при стремлении переменных 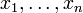 , соответственно, к
, соответственно, к 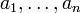 , если для каждого число
, если для каждого число 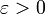 найдется такое число
найдется такое число 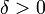 , что
, что 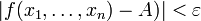 , то есть
, то есть 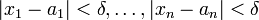 .
.
Функция 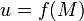 называется непрерывной в точке
называется непрерывной в точке 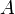 , если предельное значение этой функции в точке
, если предельное значение этой функции в точке 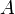 существует и равно частному значению
существует и равно частному значению 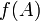 .
.
Функция 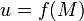 называется непрерывной на множестве
называется непрерывной на множестве 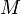 , если она непрерывна в каждой точке этого множества.
, если она непрерывна в каждой точке этого множества.
4. Частное и полное приращение функции.
Полное приращение функции
|
Частное приращение функции
|
|
Вообще, полное приращение функции не равно сумме частных приращений.
Пример.z=xy.
|
|
|
5.
| Частные производные первого порядка | |
|
Рассмотрим функцию z=f(х,у) двух независимых переменных и установим геометрический смысл частных переменных z'x=f'x(х,у) и z'y=f'y(х,у).
В этом случае уравнение z=f(х,у) есть уравнение некоторой поверхности (рис.1.3). Проведем плоскость y = const. В сечении этой плоскостью поверхности z=f(х,у) получится некоторая линия l1 пересечения, вдоль которой изменяются лишь величины х и z.
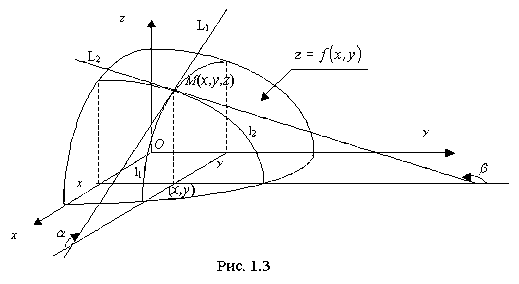
Частная производная z'x (её геометрический смысл непосредственно следует из известного нам геометрического смысла производной функции одной переменной) численно равна тангенсу угла α наклона, по отношению к оси Ох , касательной L1 к кривой l1, получающейся в сечении поверхности z=f(х,у) плоскостью y = const в точке М(х,у,f(xy)): z'x= tgα.
В сечении же поверхности z=f(х,у) плоскостью х = const получится линия пересечения l2, вдоль которой изменяются лишь величины у и z. Тогда частная производная z'y численно равна тангенсу угла β наклона по отношению к оси Оу, касательной L2 к указанной линии l2пересечения в точке М(х,у,f(xy)): z'x= tgβ.
6. Простейшие дифференциальные уравнения первого порядка — класс дифференциальных уравнений первого порядка, наиболее легко поддающихся решению и исследованию. К нему относятся уравнения в полных дифференциалах, уравнения с разделяющимися переменными, однородные уравнения первого порядка и линейные уравнения первого порядка. Все эти уравнения можно проинтегрировать в конечном виде.
Отправной точкой изложения будет служить дифференциальное уравнение первого порядка, записанное в т. н. симметричной форме:
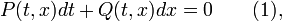
где функции 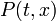 и
и 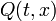 определены и непрерывны в некоторой области
определены и непрерывны в некоторой области 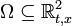 .
.
Выясним каков геометрический смысл дифференциала. Возьмем на графике функции y = f(x) произвольную точку M(x,y) (рис21.). Проведем касательную к кривой y = f(x) в точке M, которая образует угол f с положительным направлением оси OX, то есть f'(x) = tg f. Из прямоугольного треугольника MKN
KN = MNtgf = D xtg f = f'(x)D x,
то есть dy = KN.
Таким образом, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции y = f(x) в данной точке, когда x получает приращение D x.
7. Рассмотрим для примера функцию
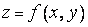
от двух переменных, которую будем предполагать дифференцируемой.
Мы хотим вычислить эту функцию в точке 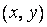 , где
, где
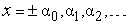 ,
,
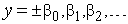 ,
,
Приближенные значения этих чисел запишем в виде конечных десятичных дробей
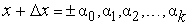 ,
,
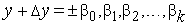 .
.
Таким образом, имеют место приближенные равенства

с абсолютными погрешностями приближения, удовлетворяющими неравенствам
 .
.
Подставив в функцию 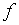 вместо
вместо 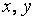 соответственно
соответственно  , получим приближенное равенство
, получим приближенное равенство
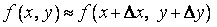
с абсолютной погрешностью
 ,
,
которую при достаточно малых 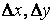 можно приближенно заменить дифференциалом функции
можно приближенно заменить дифференциалом функции 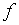 в точке
в точке 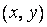 :
:
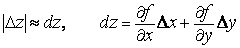 .
.
Отсюда получаем неравенство
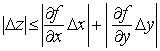 . (1)
. (1)
На самом деле это неравенство приближенное, потому что мы получили его, пренебрегая некоторой величиной, правда, значительно меньшей, чем 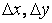 .
.
Обратим внимание на тот факт, что конечные десятичные дроби 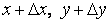 при уменьшении
при уменьшении 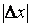 ,
, 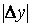 становятся все более и более громоздкими. Поэтому при вычислении числа
становятся все более и более громоздкими. Поэтому при вычислении числа 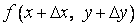 мы должны беспокоиться не только о том, чтобы оно приближало
мы должны беспокоиться не только о том, чтобы оно приближало 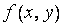 должным образом, но и чтобы производимые при этом вычисления совершались возможно, экономно. В силу этого замечания из неравенства (1) следует, что если нужно, чтобы абсолютная погрешность
должным образом, но и чтобы производимые при этом вычисления совершались возможно, экономно. В силу этого замечания из неравенства (1) следует, что если нужно, чтобы абсолютная погрешность 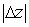 не превышала данную малую величину, которую мы обозначим через
не превышала данную малую величину, которую мы обозначим через 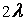 , то этого мы достигнем, взяв числа
, то этого мы достигнем, взяв числа 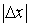 ,
, 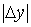 такими, чтобы выполнялись неравенства
такими, чтобы выполнялись неравенства
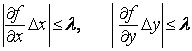 , (2)
, (2)
т. е. чтобы погрешность 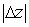 распределялась между слагаемыми в правой части неравенства (1) поровну.
распределялась между слагаемыми в правой части неравенства (1) поровну.
Из неравенств (2) видно, что вычисления будут наиболее экономными, если в качестве 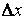 ,
, 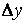 (на самом деле
(на самом деле 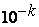 ,
, 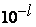 ) взять наибольшие возможные числа, удовлетворяющие этим неравенствам.
) взять наибольшие возможные числа, удовлетворяющие этим неравенствам.

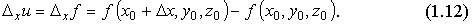 Определение 1.7 Если существует конечный предел отношения частного приращения по x функции f(x,y,z) в точке M0(x0,y0,z0) к вызвавшему его приращению Δx при Δx
Определение 1.7 Если существует конечный предел отношения частного приращения по x функции f(x,y,z) в точке M0(x0,y0,z0) к вызвавшему его приращению Δx при Δx 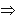 0, то этот предел называется частной производной по х функции u=f(x,y,z) в точке М0 и обозначается одним из символов:
0, то этот предел называется частной производной по х функции u=f(x,y,z) в точке М0 и обозначается одним из символов: 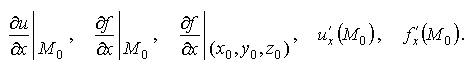 По определению,
По определению, 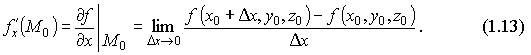 Частные производные по y и по z определяются аналогично:
Частные производные по y и по z определяются аналогично: 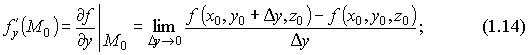
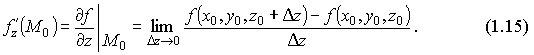 Производные f'x, f'y, f'z называются ещё и частными производными первого порядка функции f(x,y,z), или первыми частными производными. Так как частное приращение Δxf(M0) получается лишь за счет приращения независимой переменной x при фиксированных значениях других независимых переменных, то частная производная f'x(M0) может рассматриваться как производная функции f(x,y0,z0) одного переменного x. Следовательно, чтобы найти производную по x, нужно все остальные независимые переменные считать постоянными и вычислять производную по x как от функции одного независимого переменного x. Аналогично вычисляются частные производные по другим независимым переменным. Если частные производные существуют в каждой точке области V, то они будут функциями тех же независимых переменных, что и сама функция.
Производные f'x, f'y, f'z называются ещё и частными производными первого порядка функции f(x,y,z), или первыми частными производными. Так как частное приращение Δxf(M0) получается лишь за счет приращения независимой переменной x при фиксированных значениях других независимых переменных, то частная производная f'x(M0) может рассматриваться как производная функции f(x,y0,z0) одного переменного x. Следовательно, чтобы найти производную по x, нужно все остальные независимые переменные считать постоянными и вычислять производную по x как от функции одного независимого переменного x. Аналогично вычисляются частные производные по другим независимым переменным. Если частные производные существуют в каждой точке области V, то они будут функциями тех же независимых переменных, что и сама функция.