Основные сведения о конструкторах библиотеки Control System Toolbox
ХАНТЫ-МАНСИЙСКОГО АВТОНОМГОГО ОКРУГА
СУРГУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ХМАО
Кафедра автоматики и компьютерных систем
Моделирование систем
Автоматического
Управления в среде Matlab
Методические указания
По выполнению лабораторных работ
Сургут
Издательство СурГУ
Моделирование систем автоматического управления в среде Matlab: Методические указания по выполнению лабораторных работ / Сост. Д.В. Тараканов; Сургут. гос. ун-т. – Сургут: Изд-во СурГУ, 2004. – 30 с.
Методические указания соответствует государственному образовательному стандарту дисциплины «Теория автоматического управления» специальностей подготовки дипломированного специалиста 210100 (220201) «Управление и информатика в технических системах», 220400 (230105) «Программное обеспечение вычислительной техники и автоматизированных систем».
Рассмотрены методики и принципы выполнения лабораторных работ. Главное внимание уделено реализации и анализу систем автоматического управления в среде Matlab/Simulink.
Предназначены для студентов 3 курса Инженерно-физического факультета, изучающих дисциплину «Теория автоматического управления».
Табл. 9. Илл.8. Библиогр.: 3 назв.
Печатается по решению редакционно-издательского совета Сургутского государственного университета.
Рецензент А.Г. Заводовский, к.ф-м.н., доцент кафедры экспериментальной физики
ã Сургутский государственный университет, 2004
Оглавление
1. Введение…………………………………………………………….. 4
2. Моделирование систем автоматического управления с помощью библиотеки Control System Toolbox………..…………………………. 5
3. Временные и частотные характеристики систем автоматического управления………………………………………………………………14
4. Синтез систем автоматического управления……………………… 20
5. Релейный регулятор уровня жидкости в резервуаре……………... 25
Список литературы…………………………………………………….. 29
ВВЕДЕНИЕ
Система MatLab (Matrix Laboratory) [1-3] является высоко точной системой математических вычислений и в настоящее время наиболее мощной средой универсального моделирования. Пакет прикладных программ (ППП) MatLab основан на современных высокоэффективных алгоритмах матричных операций. Программа MatLab имеет открытую архитектуру, что дает доступ пользователям к ее кодам.
Matlab взаимодействует c визуально - ориентированным средством динамического моделирования Simulink. Данная среда позволяет эффективно реализовать динамические модели систем на основании встроенной библиотеки.
В структуре программы моделирования Matlab содержится большое количество библиотек – Toolbox, специализирующихся на выполнении различных математических, технических и экономических задачах.
При реализации библиотеки Control System Toolbox пакета использованы принципы объектно-ориентированного программирования. Введен новый класс объектов: линейные системы с постоянными параметрами (liner time invariant objects, или lti-объекты). Этот класс включает линейные непрерывные или дискретные, одномерные с одним входом и одним выходом (SISO-системы) и многомерные со многими входами и (или) многими выходами (MIMO-системы). Каждому объекту присваивается определенный идентификатор.
Модель lti-системы в теории автоматического управления может быть задана:
· четверкой матриц {A, B, C, D}, которая описывает дифференциальное (или разностное) векторное уравнение системы в пространстве состояний в явной форме Коши;
· двумя векторами, задающими коэффициенты многочленов числителя и знаменателя передаточной функции системы;
· двумя векторами и одним числом, задающими нули, полюсы и обобщенный коэффициент передачи передаточной функции системы.
В соответствии с этим lti-система в ППП The Control System Toolbox может быть представлена тремя подклассами:
· четверкой матриц – подкласс ss в пространстве состояний;
· двумя векторами, составленными из коэффициентов числителя и знаменателя, - для одномерных систем, или двумя массивами ячеек, содержащих векторы коэффициентов, - для многомерных систем, что соответствует подклассу tf (передаточная функция в виде отношения многочленов либо матрица таких передаточных функций);
· двумя векторами, составленными из нулей и полюсов передаточной функции, и скаляром, равным обобщенному коэффициенту передачи, - для одномерных систем, или двумя массивами ячеек, содержащих векторы, составленные из нулей и полюсов, и массивом чисел – для многомерных систем, что соответствует подклассу zpk (передаточная функция в виде нулей, полюсов и обобщенного коэффициента передачи либо матрица таких передаточных функций).
Модель системы, заданная в одном из этих подклассов, может быть преобразована в любой другой подкласс.
МОДЕЛИРОВАНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ С ПОМОЩЬЮ БИБЛИОТЕКИ CONTROL SYSTEM TOOLBOX.
Цели лабораторной работы
Получение навыков организации моделей в различных математических базисах и проведения анализа САУ с помощьюбиблиотеки Control System Toolbox.
Основные сведения о конструкторах библиотеки Control System Toolbox
Библиотека Control System Toolbox для описания непрерывных и дискретных динамических моделей систем управления с постоянными параметрами использует либо tf–форму передаточной функции, либо zpk-форму нулей, полюсов и обобщенного коэффициента передачи, либо ss-форму пространства состояний. Передаточная функция описывается в виде отношения многочленов, которые задаются в виде векторов-строк, составленных из их коэффициентов. В zpk-форме корни многочленов числителя и знаменателя передаточной функции и обобщенного коэффициента передачи также задаются в виде одномерных массивов. Наиболее естественным для системы MatLab является представление модели в пространстве состояний в виде дифференциального или разностного уравнения. Модели могут быть одномерными (с одним входом и одним выходом - SISO) или многомерными (со многими входами и многими выходами - MIMO).
Таким образом, математическую модель стационарной непрерывной иди дискретной системы можно задать следующими способами:
· в tf–форме передаточной функции
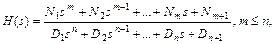
при описании дискретных систем комплексная переменная s заменяется
на z;
· в zpk-форме нулей, полюсов и коэффициента усиления
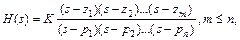
· в ss-форме пространства состояний в виде системы дифференциальных уравнений
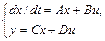
При описании дискретных систем в виде совокупности разностных уравнений необходимо задавать время квантования сигнала.
Функции формирования и преобразования моделей систем управления представлены в таблице 2.1.
Таблица 2.1
