Общие сведения. Уравнение равновесия элемента трубы

Если толщина стенки трубы, нагруженной радиальной на­грузкой, превышает 0,1 радиуса геометрической оси стенки, труба считается толстостенной. Распределение напряжений по толщине стенки такой трубы нельзя считать равномерным; радиальные пере­мещения отдельных точек стенки трубы зависят от их расстоя­ния r до оси трубы.

С помощью теории расчета толстостенных труб определяются напряжения и перемещения в точках стенок цилиндров машин, стволов орудий, при температурных или прессовых посадках рубашек, муфт и ступиц на валы, а также в облицовках тоннелей и стволов, подверженных горному давлению.

Рассмотрим отрезок трубы длиной, равной единице, вырезанный двумя сечениями, нормальными к оси трубы (рис. 30,а). Труба нагружена на внутренней и наружной поверхностях радиальной сжимающей нагрузкой; интенсивности р_В и р_Н этой нагрузки по­стоянны как вдоль оси трубы, так и по ее окружности. Любой такой отрезок на некотором расстоянии от торцов трубы находится в плоском деформированном состоянии.

А б

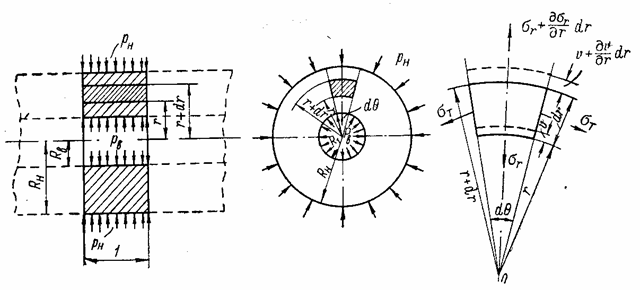
Рис. 30

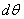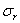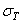Составим уравнение равновесия элемента трубы, выделенного двумя радиальными сечениями, составляющими между собой угол , и двумя окружными сечениями, радиусы которых r и r + dr (рис. 30,б). По граням этого элемента действуют радиаль­ные и окружные напряжения и . Радиальное напряжение при изменении радиусаr получает приращение 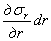, а окружное напряжение 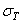в силу осевой симметрии задачи при изменении угла 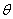не меняется.

Дифференциальное уравнение равновесия (1.32,б) для осесимметричной задачи имеет вид

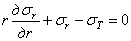. (3.1)

Напря­жения 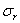и 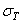выразим через относительные линейные деформа­ции 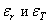с помощью закона Гука:

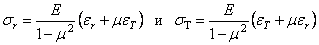, (3.2)

а относительные деформации заменим их выраже­ниями через радиальное перемещение v (рис. 30,б), пользуясь зависимостями

.

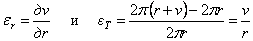Подставив эти выражения в формулу (3.2), а выражения (3.2) в фор­мулу (3.1), получим выражения для напряжений и дифферен­циальное уравнение равновесия элемента трубы в перемещениях

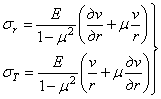, (3.3)

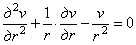. (3.4)

Уравнение (3.4) может быть представлено в виде

,

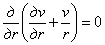откуда следует, что

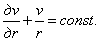
Этому уравнению удовлетворяет решение

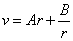. (3.5)

Заменив в формулах (3.3) перемещение v его выражением (3.5), получим для напряжений:

. (3.6)

Граничные условия для определения постоянных А и В со­ставляем из условий на внутренней и наружной поверхностях трубы:

1) 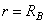, 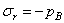; 2) , .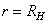

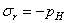Учет этих условий в первом уравнении (3.6) дает систему двух уравнений, содержащих А и В, решив которую, найдем

.

Подстановка найденных значений А и В в уравнения (3.6) дает следующие выражения для напряжений:

, (3.7)

а подстановка в уравнение (3.5) - выражение для радиального пере­мещения

(3.8)

В формулах (3.7) и (3.8)

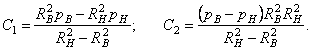
Из формул (3.7) видно, что

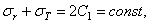
т. е. сумма радиального и окружного напряжений в любой точке есть постоянная величина, не зависящая от радиуса r.

По формулам (3.7) и (3.8) можно вычислить напряжения и радиальные перемещения для сплошного вала, подверженного наружному радиальному давлению, если положить R_B = 0. В та­ком случае

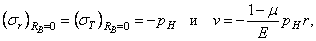
откуда видно, что материал вала испытывает однородное напря­женное состояние.