Дисконтирование и учет по простым процентным ставкам
Дисконтирование означает приведение стоимостного показателя, относящегося к будущему, на некоторый, более ранний момент времени.
Данная задача является обратной наращению процентов: по величине S определяется Р.
В этом случае говорят, что сумма S дисконтируется или учитывается, сам процесс начисления процентов и их удержание называют учетом, а удержанные проценты – дисконтом.
Величину Р, найденную с помощью дисконтирования, называют современной капитализированной стоимостью.
В зависимости от вида процентной ставки применяют два вида дисконтирования:
• математическое дисконтирование;
• банковский (коммерческий) учет.
1. Математическое дисконтирование. В этом случае рассчитывается значение дисконтного множителя и дисконт (D) с суммы долга (S):
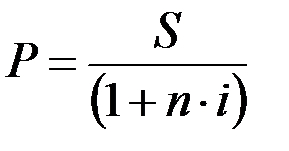, (17.6)
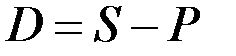. (17.7)
Таким образом, решается задача, обратная задаче наращения первоначальной суммы ссуды: определяется, какую первоначальную сумму надо дать в долг, чтобы получить в конце срока сумму S при условии, что на долг начисляются проценты по ставке i. Дисконтный множитель, равный 1/(1+ni), показывает, какую долю составляет первоначальная величина долга в его окончательной сумме.
2. Банковский или коммерческий учет. В этом виде дисконтирования проценты начисляются на сумму, подлежащую уплате в конце срока, согласно учетной ставке d:
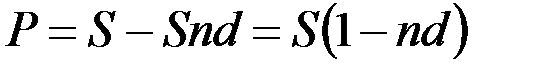, (17.8)
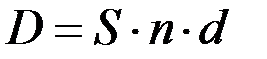. (17.9)
Дисконтный множитель равен (1–nd). Простая учетная ставка применяется иногда при расчете наращенной суммы.
Если известна текущая сумма долга и требуется определить его будущую стоимость, то при использовании учетной ставки:
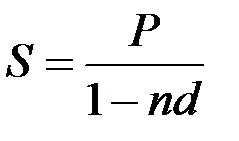(17.10)
где 1/(1+nd) – множитель наращения.
Сложные проценты
В среднесрочных и долгосрочных финансово-кредитных операциях, если проценты не выплачиваются сразу же после их начисления, а присоединяются к сумме долга, для наращения применяются сложные проценты. База для начисления сложных процентов увеличивается с каждым периодом выплат.
Присоединение начисленных процентов к сумме долга, которая служит базой для их начисления, называют капитализацией процентов.
Формула для расчета наращенной суммы в конце n-го года при условии, что проценты начисляются один раз в году, имеет вид:
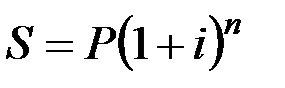(17.11)
где Р – первоначальный размер долга;
i – ставка наращения по сложным процентам;
n – число лет наращения.
Величина q = (1 + i)n называется множителем наращения по сложным процентам, а формула (17.11) является основной формулой сложных процентов.
Необходимо отметить, что основная формула сложных процентов (17.11) предполагает постоянную процентную ставку на протяжении всего срока начисления процентов.