Локальная и интегральная теоремы Лапласа
Пусть производится n одинаковых независимых испытаний с вероятностью появления события в каждом испытании, равной p. Тогда вероятность частоты m наступления события А определяется, как было показано ранее по формуле Бернулли:
.
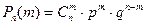Вычисление по этой формуле трудно практически осуществить при n > 20.
В таких случаях применяют асимптотическую формулу, позволяющую найти указанную вероятность. Теорема, выражающая эту формулу, носит название локальной теоремы Муавра – Лапласа.
Теорема. Если производится n одинаковых испытаний, в каждом из которых вероятность появления события равна p, то вероятность того, что данное событие появится m раз, определяется по формуле
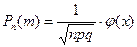, где 
; 
.
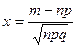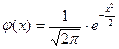Эта теорема дает приближение биномиального закона распределения к нормальному при p, значительно отличающемся от нуля и единицы.
Задача. Для мастера определенной квалификации вероятность изготовить деталь отличного качества равна 0,75. За смену он изготовил 400 деталей. Найти вероятность того, что в их числе 250 деталей отличного качества.
Решение: По условию n = 400, p = 0,75 , q = 0,25 и m = 280, откуда npq = 75, х = –2,3095.
По таблицам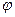 
(t) найдем 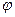(–2,31) = 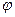(2,31) = 0,0277. Искомая вероятность равна Р = 0,0032.
Интегральная теорема Лапласа
Для вычисления вероятности того, что частота m, подчиненная биномиальному закону распределения, заключена между данными значениям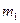и 
и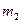 
, применяют интегральную теорему Лапласа, выраженную асимптотической формулой. Формулу, выражающую интегральную теорему Лапласа, можно получить из закона нормального распределения.
Теорема. Пусть вероятность р наступления события А в каждом испытании постоянна и 0 < p < 1. Тогда вероятность того, что событие А появится в n испытаниях от 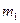до 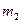раз, приближенно равна определенному интегралу
= 
,
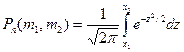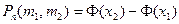где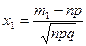 
, 
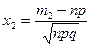и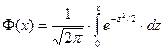 
.
При больших значениях n наиболее вероятная частота совпадает с математическим ожиданием частоты. Поэтому для нахождения вероятности того, что абсолютная величина отклонения частоты от наиболее вероятной частоты не превосходит заданного числа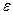 
> 0, используют приближенное равенство:
.
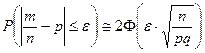Формула Пуассона
Если вероятность события р (или q) в отдельном испытании близка к нулю, то даже при большом числе испытаний n, но небольшой величине произведения np (меньше 10), применяют асимптотическую формулу Пуассона
,
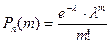где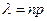 
.
Задача. Некоторое электронное устройство выходит из строя, если откажет определенная микросхема. Вероятность ее отказа в течение 1 ч работы устройства равна 0,004. Какова вероятность того, что за 1000 ч работы устройства придется пять раз менять микросхему?
Решение: По условию, n = 1000, p = 0,004, а 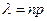= 1000 • 0,004 = 4 < 10. Для нахождения вероятности P1000(5) воспользуемся формулой Пуассона, так как условия ее применения выполнены. Имеем
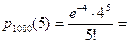0,1582.
Задача. На факультете насчитывается 1825 студентов. Какова вероятность того, что 1 сентября является днем рождения одновременно четырех студентов факультета?
Решение: Вероятность того, что день рождения студента 1 сентября, равна р = 1/365. Так как р = 1/365 – мала , n = 1825 – велико и l = n • р = 1825 × (1/365) = 5 £ 10, то применяем формулу Пуассона:
.
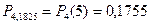