Локальная и интегральная теоремы Лапласа

Как уже было отмечено, при больших значениях n нахождение вероятности 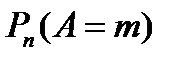превращается в технически достаточно сложную задачу. Это обстоятельство было отмечено еще в 18 веке математиками, занимающимися демографическими проблемами. Возникла необходимость получения приближенной формулы для нахождения соответствующей вероятности. Эта задача была решена для частного случая при р = 0,5 в 1730 году английским математиком Абрахамом де Муавром и обобщена в 1783 году французским математиком Пьером Лапласом.

Введем в рассмотрение следующую функцию

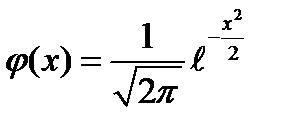(24)

Приближенные значения функции 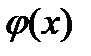для любого аргумента х можно получить, разложив ее в степенной ряд, однако, проще найти эти значения из соответствующей таблицы. При использовании этой таблицы необходимо учитывать, что функция 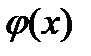четная, т.е. .

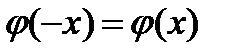Теорема 11(Локальная теорема Муавра-Лапласа). Если вероятность наступления события А в каждом из n независимых испытаний равна р и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность того, что в n испытаниях событие А наступит т раз, приближенно равна значению функци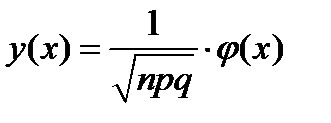и при .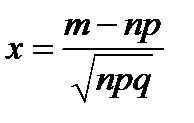

Нетрудно понять, что чем больше значение n, тем точнее получим значение вероятности.

Итак, вероятность того, что событие А появится в n испытаниях ровно т раз, приближенно равна

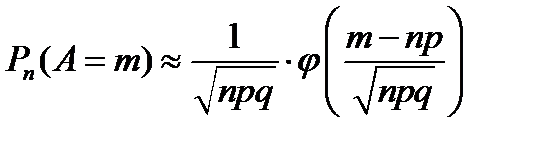(25)

Пример 21. Вероятность того, что сошедшая с конвейера деталь окажется бракованной, равна 0,1. Найти вероятность того, что из 600 деталей, сошедших с конвейера, 68 деталей окажутся бракованными.

Решение. Событие А означает, что взятая с конвейера деталь окажется бракованной. Тогда по условию задачи .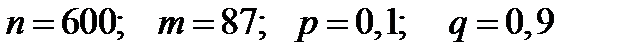

Отсюда 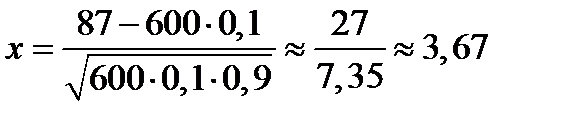и окончательно, получаем по формуле (25) с применением таблицы значений функции (24):

. ■

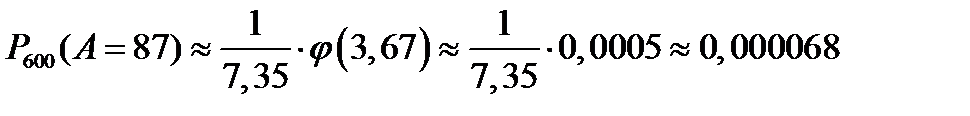Пример 22. Вероятность поражения мишени стрелком при одном выстреле р = 0,7. Найти вероятность того, что при 20 выстрелах стрелок поразит мишень 15 раз.

Решение. Событие А означает, что стрелок попадет в мишень при одном выстреле. Тогда по условию 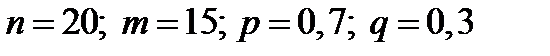. По формуле (10.25) получаем

.

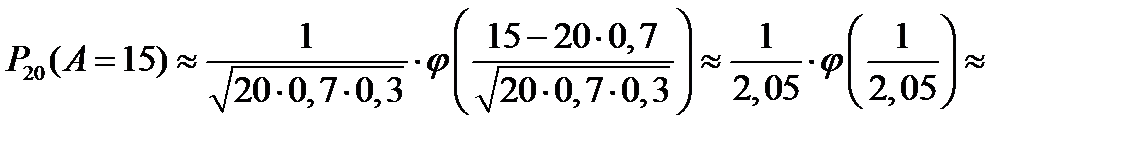
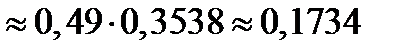Найдем ту же вероятность, применяя формулу Бернулли, получим

. ■

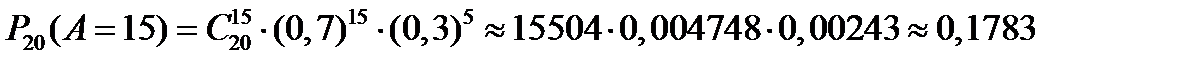В последнем примере вероятности одного и того же события, найденные по разным формулам, имеют разные значения, так как формула (10.25) дает лишь приближенное значение этой вероятности. Однако, очевидно, что расхождение в ответах не очень велико. Неплохую точность ответа, найденного по формуле (25), обеспечило, в частности, то, что вероятность р появления события А не является малой. При малых значениях вероятности р рекомендуется применять для решения выше рассмотренных задач формулу Пуассона.

Предположим, что вероятность р появления события А в отдельном испытании близка к нулю. Такие события А называются редкими. Тогда даже при большом числе испытаний, но небольшой величине произведения np (меньше 10) вероятность, полученная по формуле (25) будет недостаточно близка к своему истинному значению. В таких случаях применяют другую приближенную формулу, называемую формулой Пуассона.

Теорема 12 (Теорема Пуассона). Если вероятность р появления события А в каждом испытании постоянна, но близка к нулю, число независимых испытаний Бернулли достаточно велико, то вероятность того, что в этих n испытаниях событие А наступит ровно т раз, приближенно равна

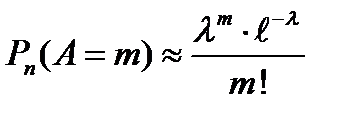, (26)

где .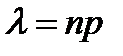

Отметим, что имеются специальные таблицы, пользуясь которыми можно найти вероятность 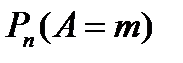для конкретных значений n и т.

Формула (26) называется формулой Пуассона.

Пример 23. Завод отправил в магазин 5000 исправных телевизоров.
Вероятность того, что во время пути произойдет повреждение телевизора, равна 0,0002. Какова вероятность того, что во время пути произойдут повреждения у трех телевизоров? Найти вероятность по разным формулам и сравнить полученные результаты.

Решение. Событие А означает, что во время пути один телевизор получил повреждение. Тогда по условию примера 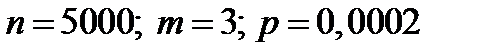. Вероятность появления события А – поломка в пути одного телевизора, очень мала. Произведение 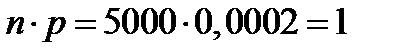также мало. Применим формулу (10.26), получим .

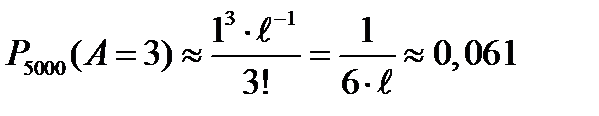Найдем ту же вероятность по формуле (25), используя локальную теорему Муавра-Лапласа, получим

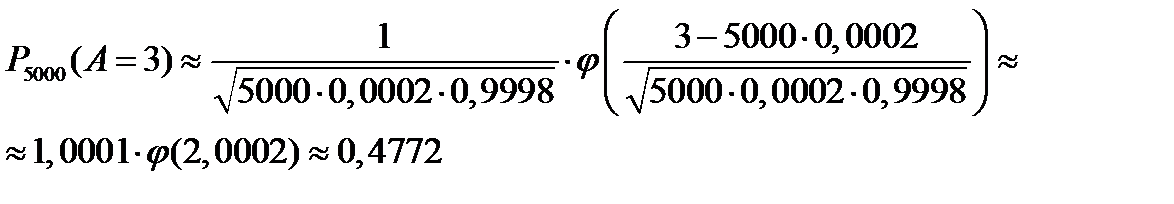
Нетрудно видеть, что расхождение в ответах очень большое. Проверим, какая из формул дает более точный результат. Для этого найдем ту же вероятность по формуле Бернулли, получим

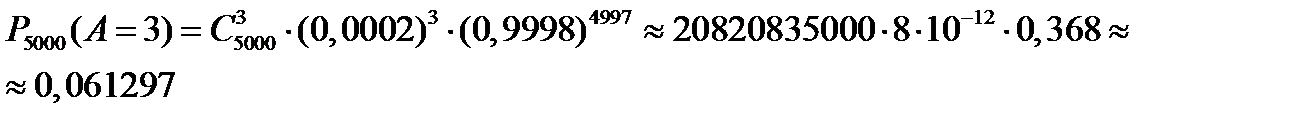
Очевидно, что формула Пуассона дает практически такой же результат, что и формула Бернулли, а формулу Муавра-Лапласа в этих условиях применять не рекомендуется. ■

Локальная теорема Муавра-Лапласа и теорема Пуассона дают формулу, которая является приближением формулы (18). Аналогичную формулу можно предложить и для (22).

Вновь предположим, что проводится n испытаний Бернулли и надо найти вероятность того, что в этих испытаниях событие А появится не менее т₁ раз и не более т₂ раз, при этом будем предполагать, что число испытаний достаточно велико.

Введем в рассмотрение следующую функцию.

Функцией Лапласа называется функция вида

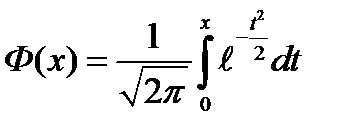(27)

Неопределенный интеграл 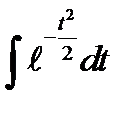не выражается через элементарные функции, поэтому для нахождения соответствующего определенного интеграла и значений самой функции Лапласа пользуются специальными таблицами. В таблице даны значения для положительных аргументов и нуля. Для отрицательных значениях х используют ту же таблицу, учитывая, что функция Лапласа является нечетной, т.е. .

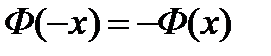Теорема 13 (Интегральная теорема Лапласа).Вероятность того, что в независимых испытаниях, в каждом из которых вероятность появления события А равна р (0 < p < 1), событие А наступит не менее т₁ раз и не более т₂ раз, приближенно равна

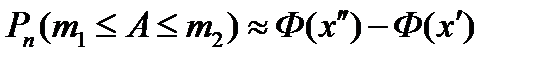, (28)

где .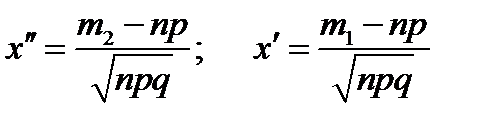

Пример 24. Вероятность того, что деталь не прошла проверку ОТК, равна 0,1. Найти вероятность того, что среди случайно отобранных 500 деталей проверку не пройдут от 70 до 100 деталей.

Решение. Событие А означает, что одна деталь не прошла проверку ОТК. Тогда по условию .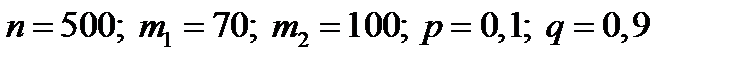

Воспользуемся интегральной теоремой и формулой (10.28), получим

. ■

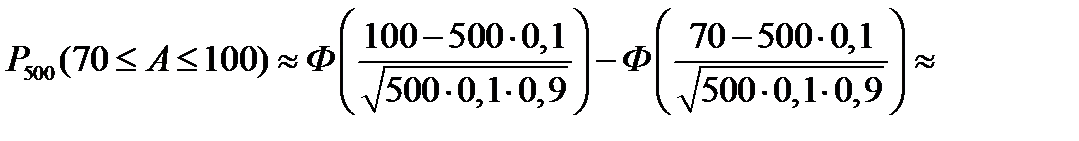
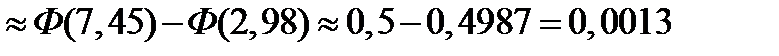Помимо случайного события основным элементом теории вероятностей является также случайная величина, т.е. величина, которая случайным образом принимает в результате испытания одно значение из множества возможных.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Понятие случайного события, виды событий. Пространство элементарных событий. Примеры.

2. Совместные и несовместные события. Полная группа событий для данного испытания. Противоположные события. Примеры.

3. Основные операции над случайными событиями. Примеры.

4. Статистическое определение вероятности случайного события. Основные свойства вероятности события.

5. Классическая формула определения вероятности.

6. Комбинаторика и ее основные правила.

7. Основные элементы комбинаторики и их число.

8. Теорема сложения вероятностей и ее применение.

9. Понятие условной вероятности события. Зависимые и независимые
события.

10. Теорема умножения вероятностей и ее применение. Следствие.

11. Формула полной вероятности.

12. Априорные и апостериорные вероятности. Формулы Байеса.

13. Определение испытаний Бернулли. Пример.

14. Формула Бернулли и ее частные случаи.

15. Локальная теорема Муавра-Лапласа.

16. Теорема Пуассона.

17. Интегральная теорема Лапласа.