Реальное дифференцирующее звено
Передаточная функция
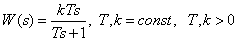 .
.
Преобразуем передаточную функцию реального дифференцирующего звена для удобства получения временных характеристик –
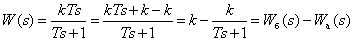 .
.
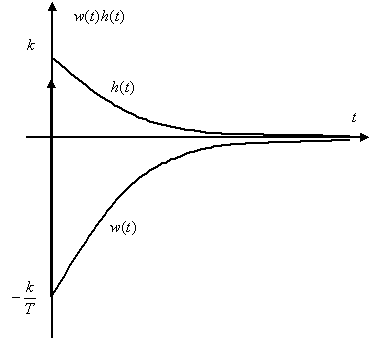
Временные характеристики можно определить по известным характеристикам безынерционного и апериодического звеньев –
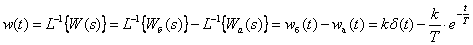 ,
,
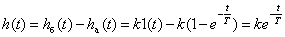 .
.
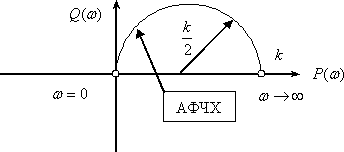
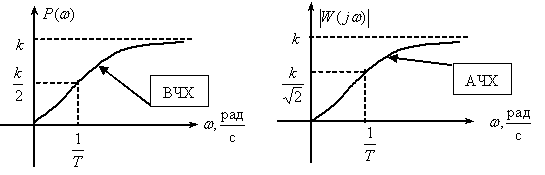
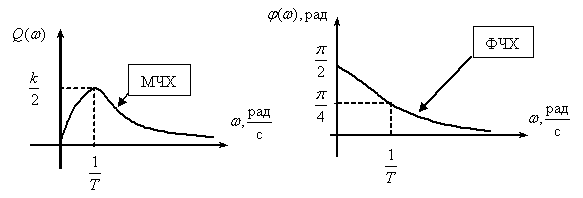
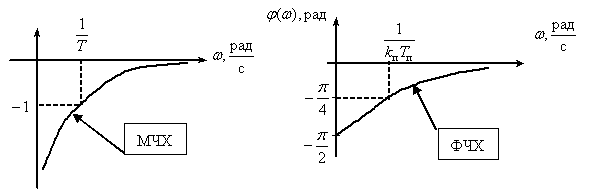
Частотная характеристика
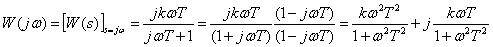 ,
,
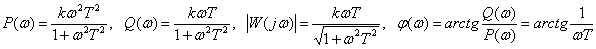 .
.
Интегрирующее звено с запаздыванием
Передаточная функция
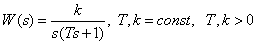 .
.
Преобразуем передаточную функцию реального дифференцирующего звена для удобства получения временных характеристик –
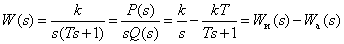 ,
,
где
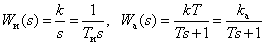 .
.
Временные характеристики можно определить по известным характеристикам интегрирующего и апериодического звеньев –
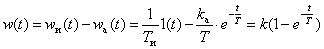 ,
,
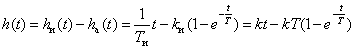 .
.
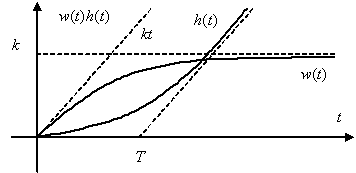
Частотная характеристика
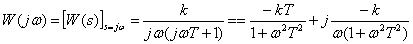 ,
,
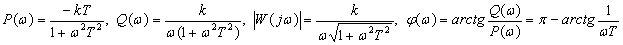

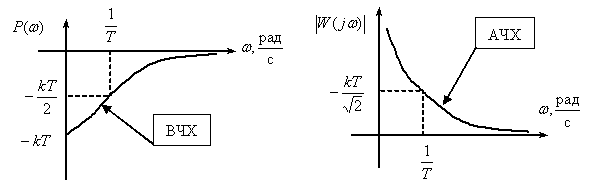
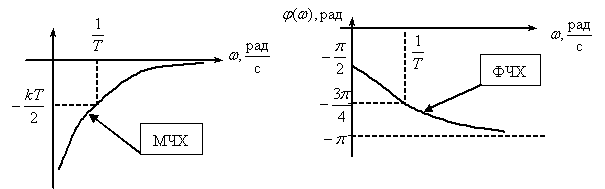
Пропорционально-интегрирующее звено
Передаточная функция
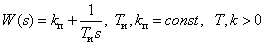 .
.
Временные характеристики можно определить по известным характеристикам безынерционного и интегрирующего звеньев –
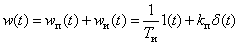 ,
,
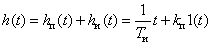 .
.
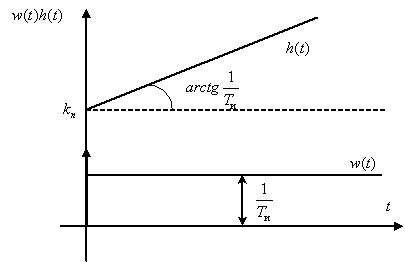
Частотная характеристика
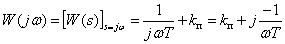 ,
,
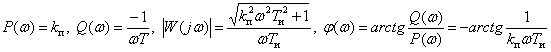 .
.
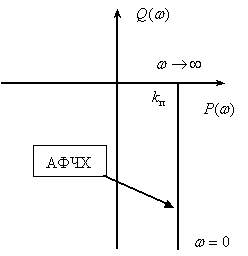
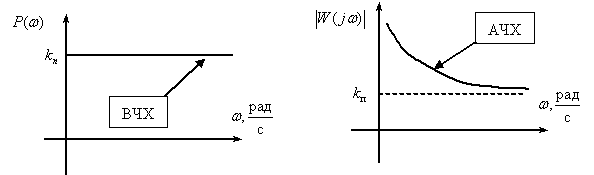
Приложение А
(справочное)
Таблица соответствия оригиналов и изображений
Таблица А.1
| Изображение X(s) | Оригинал x(t) | |
| ke–τs | k∙1(t–τ) запаздывание на τ > 0 | |
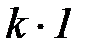 | импульсная функция k∙δ(t) | |
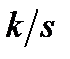 | – простой нулевой корень | скачок k∙1(t) или просто k |
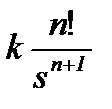 | – кратный нулевой корень | k∙tn – степенной ряд от t |
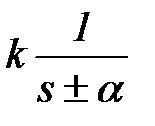 | – простой действительный корень | 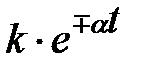 – экспонента – экспонента |
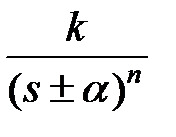 | – кратный действительный корень | 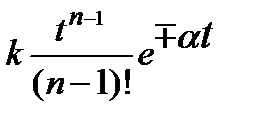 , при n > 1 , при n > 1 |
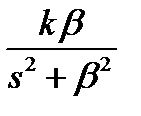 | – сопряженные мнимые корни | k∙sinβt – гармоническая функция |
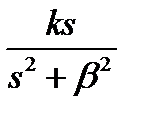 | – сопряженные мнимые корни | k∙cosβt – гармоническая функция |
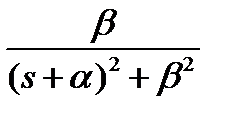 | 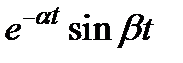 - затухающая гармоническая функция - затухающая гармоническая функция | |
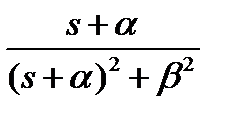 | 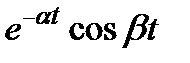 - затухающая гармоническая функция - затухающая гармоническая функция | |
сопряженные комплексные корни 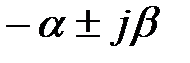 , объединенные в одну дробь , объединенные в одну дробь 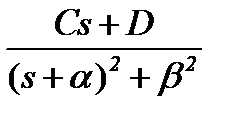 , с вычислением , с вычислением 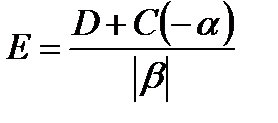 | а) предпочтительная форма 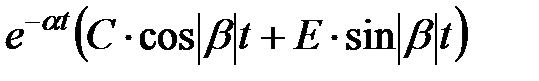 б) через синус (угол в радианах) б) через синус (угол в радианах) 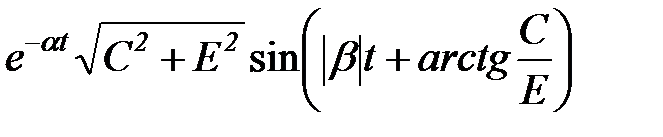 в) через косинус (угол в радианах) в) через косинус (угол в радианах) 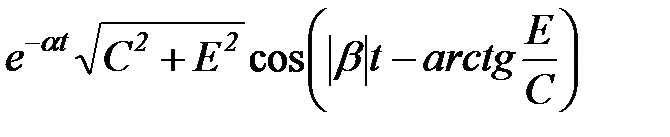 | |
сопряженные комплексные корни (раздельное представление) 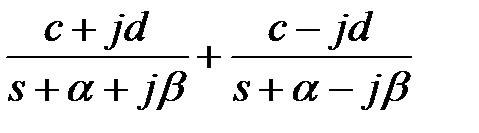 | 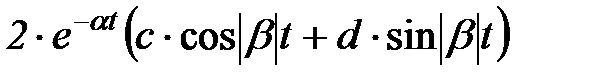 перед d ставят плюс, если знаки мнимых частей изображения в числителе и знаменателе совпадают (как показано), а иначе минус перед d ставят плюс, если знаки мнимых частей изображения в числителе и знаменателе совпадают (как показано), а иначе минус |
Примечание – Даже если скачок 1(t) в формуле для входной функции не пишется, то всегда подразумевается, т.к. по Лапласу при t = 0- любая функция f(t) равна нулю, а затем она появляется скачком. Однако сомножитель 1/s вводят в изображение входной функции лишь в том случае, если она представляет собой чисто ступенчатое воздействие, даже если в функциях-оригиналах другого вида скачок и был указан.
Приложение Б
(справочное)
