Применение регрессионного анализа в ходе принятия решения

Выполнение работы

Записываем исходные данные и формулу для расчета суммы выплат, как и в первом задании. Затем создаем таблицу с данными. Для этого пишем заголовки столбцов, затем - в ячейке С2 записываем формулу =В3, в ячейку В8 -формулу =В4, в ячейку С8 - формулу =В5. Для расчета процента от 15% до 20% с шагом 0,5% записываем формулу =A8+0,005 и копируем ее вниз по столбцу, пока не получим значение 20%. Затем выделяем диапазон ячеек A8:c10 щелкаем на пункте меню Данные → Таблица подстановки и в окошке Подставлять значения по строкам в записываем адрес ячейки с процентной ставкой:

После нажатия на ОК получим следующую таблицу:

	А	В	Формулы:
	Размер	850 000грн.
	Срок вклада
	процент. Ставка	10%	0,1
	коэффициент наращения	4,177248169	=B5/B1
	Сумма выплаты	3 550 660,94грн.	=БЗ(B3;B2;0;-B1;0)
	процент. Ставка	Коэфф	Сумма выплаты
	15,0%	4,18	3 550 660,94грн.
	15,5%	8,68	7 381 569,09грн.
	16,0%	9,27	7 875 692,74грн.
	16,5%	9,88	8 400 551,65грн.
	17,0%	10,54	8 957 913,24грн.
	17,5%	11,23	9 549 638,35грн.
	18,0%	11,97	10 177 685,70грн.
	18,5%	12,76	10 844 116,66грн.
	19,0%	13,59	11 551 100,08грн.
	19,5%	14,47	12 300 917,48грн.
	20,0%	15,41	13 095 968,34грн.

Таблица вариантов

№	Размер вклада	Срок вклада	Процентная ставка	№	Размер вклада	Срок вклада	Процентная ставка
			10,0%				9,0%
			9,0%				8,0%
			8,0%				7,0%
			7,0%				6,0%
			6,0%				5,0%
			5,0%				4,0%
			4,0%				3,0%
			5,5%				4,5%
			7,0%				6,0%
			8,5%				7,5%
			10,0%				9,0%
			11,5%				10,5%
			10,5%				9,5%
			9,5%				8,5%
			8,5%				7,5%

Задание №3

Директор фірми повинен скласти штатний розпис, тобто визначити, скільки працівників, на яких посадах і з яким окладом він повинен прийняти на роботу. Загальний місячний фонд зарплати складає 100000 грн.

Для нормальної роботи фірми необхідно 9 продавців, 3 старших продавців, 5 менеджерів для роботи з товарами, 2 завідувачі відділами, 1 менеджер з вивчення кон'юнктури ринку, 1 завідувач складом, 1 головний менеджер, 1 директор. Оклад продавцеві встановили в розмірі 1500 грн., старший продавець повинен отримувати в 1,5+0,1*n рази більше продавця, менеджер по роботі з товарами – в 3+0,1*n рази більше від продавця, заввідділом – на 300+10*n грн. більше, ніж менеджер по роботі з товарами, менеджер з вивчення кон'юнктури ринку – в 2+0,1*n рази більше від продавця, завскладом на 200+10*n грн. більше від старшого продавця, головний менеджер – в 4+0,1*n рази більше від продавця, директор універмагу – на 2000+n грн. більше від головного менеджера,

де n – номер за журналом.

При розв'язку задачі необхідно врахувати, що за основу береться оклад продавця, а всі інші обчислюються через нього – у скільки разів або на скільки більше, тобто кожний оклад є лінійною функцією від окладу продавця:

А*П + В,

де П – оклад продавця,

Із умови задачі видно, що коефіцієнти А і В приймають наступні значення:

А = 1 В = 0

А = 1,5+0,1*n В = 0

А = 3+0,1*n В = 0

А = 2+0,1*n В = 0

А = 1,5+0,1*n В = 400+ n*10

А = 4+0,1*n В = 0

А = 3+0,1*n В = 300+ n*10

А = 4+0,1*n В = 2000+ n*100

Задавши кількість людей на кожну посаду, можна скласти рівняння:

N1*(А1*П+Bl) + N2*(А1*П+Bl) + ...+N8*(А1*П+Bl),

де N1 – кількість продавців;

N2 – кількість старших продавців;

А1...А8 і В1...В8 – коефіцієнти для кожної посади.

1. Для розв'язку задачі створіть таблицю такої форми

Розрахунок фонду зарплати продавців універмагу

	А	В	С	D	Е	F	G	Н
	Коефіцієнт А	Коефіцієнт В	Посада	Зарплата	Кількість працівників	Сумарна зарплата		Зарплата продавця
			Продавець				1500,00
			Ст. продавець
			Менеджер по роботі з товарами
			Менеджер вивчення кон'юнктури ринку
			Зав. складом
			Гол. менеджер
			Зав. відділом
			Директор
	Сумарний місячний фонд зарплати

1.1. Заповніть шапку таблиці.

1.2. Відведіть для кожної посади один рядок і занесіть в стовпчик С назви посад.

1.3. В стовпчиках А і В вкажіть коефіцієнти А і В, які відповідають кожній посаді.

1.4. В клітинку НЗ занесіть значення заробітної плати продавця (1500) і встановіть для неї формат 0,00 – два знаки після коми.

2. В стовпчику D обчисліть заробітну плату для кожної посади.

2.1. В клітинку D3 занесіть формулу =АЗ*$Н$3+В3

2.2. Скопіюйте формулу із клітинки D3 на діапазон D4:D10.

3. В стовпчику Е вкажіть кількість працівників на посадах.

4. В стовпчику F обчисліть заробітну плату всіх працівників, які займають дану посаду.

4.1. В клітинку F3 занесіть формулу =D3*E3 (зарплата * кількість працівників).

4.2. Скопіюйте формулу із клітинки F3 на діапазон F4:F10.

4.3. Встановіть для даних в стовпчиках D і F формат 0,00 – два знаки після коми.

5. Визначить сумарний місячний фонд заробітної плати.

5.1. Просумуйте дані в стовпчику F, використовуючи інструмент автосумування.

5.2. Перемістіть значення суми в клітинки F12 і зробіть до неї підпис. «Сумарний місячний фонд заробітної плати».

Завдання:Визначити, при якій зарплаті продавця сумарний місячний фонд заробітної плати буде дорівнювати заданому - 100000 грн. (в комірці F12 необхідно отримати значення ≈ 100000).

Використання процедуриПідбір параметру:

1. Виберіть з меню Сервис пункт Подбор параметра.

2. Вкажіть в полі Установить в ячейке адресу цільової клітинки $F$12.

3. Вкажіть в полі Значение – 100 000.

4. Вкажіть в полі Изменяя ячейку адресу клітинки із заробітною платою продавця $Н$3 і натисніть на клавішу ОК.

Збережіть таблицю в особистому каталозі під іменем яке задаєте самі.

Задание № 4

ПРИМЕНЕНИЕ РЕГРЕССИОННОГО АНАЛИЗА В ХОДЕ ПРИНЯТИЯ РЕШЕНИЯ

Регрессионный анализ – очень эффективный метод, способный помочь в анализе больших объёмов данных. Его можно применять при принятии решений по многим вопросам, начиная с финансирования операций вашей фирмы и комиссионных, полученным от продажи, и заканчивая проведением маркетинговых исследований.

На рис. 1 показаны две переменные – смета на рекламу и объёмы продаж в единицах продукции – для 18 видов продукции, проданной компанией. Здесь также изображена диаграмма, показывающая связь между сметой на рекламу и объёмом продаж в единицах продукции.

1.Выделите данные в диапазоне А2:В20.

2.Выберите команду ВставкаÞДиаграммаÞНа этом листе либо щёлкните на кнопке Мастер диаграмм.

3.Выделите область построения диаграммы на рабочем листе.

4.На шаге 1 работы средства Мастер диаграмм проверьте, что в текстовом поле Диапазон введены адреса ячеек, содержащих данные для построения диаграммы. Щёлкните на кнопке Далее.

5.На шаге 2 работы средства Мастер диаграмм выберите тип диаграммы (график). Щёлкните на кнопке Далее

6.На шаге 3 работы средства Мастер диаграмм выберите вид графика. Щёлкните на кнопке Далее.

7.На шаге 4 работы средства Мастер диаграмм убедитесь, что переключатель Ряды данных находятся установлен в положении В столбцах. Установите значение 1 в поле Считать стлб. Метками оси Х. Щёлкните на кнопке Далее.

8.На шаге 5 работы средства Мастер диаграмм добавьте легенду и названия осей и щёлкните на кнопке Готово.

9.Когда диаграмма появиться в вашем рабочем листе, дважды щёлкните на нём для редактирования. Граница диаграммы будет заштрихованной.

10.Чтобы выбрать ряд, щёлкните на любом из маркеров ряда. Выберите команду ВставкаÞЛиния тренда и щёлкните, если необходимо, на корешке вкладки Тип. Выберите тип аппроксимации Линейная.

11.Щёлкните на корешке вкладки Параметры и проверьте, чтобы стояли флажки опций Показывать уравнение на диаграммеи Поместить на диаграмму величину достоверности аппроксимации (R$2). Щёлкните на кнопке ОК.

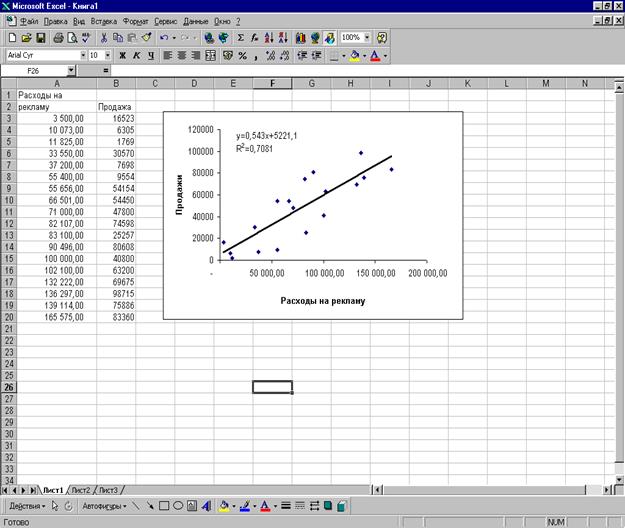
Что же вы можете узнать из информации, представленной на рисунке 1? Очевидно то, что увеличения суммы затрат на рекламу объём продаж в единицах продукции также увеличивается. Линия тренда (прямая линия, идущая от левого нижнего угла к правому верхнему) подтверждает, что эти две переменные увеличиваются пропорционально.

График также содержит следующее уравнение:

Y=0,543x + 5221,1

Это уравнение регрессии для данных в рабочем листе. Оно показывает зависимость денежной суммы, израсходованной на рекламу определённой продукции, и объёмом продаж в единицах этой продукции. В данном уравнении y означает объём продаж, оно даёт наиболее точную оценку объёма продаж в единицах продукции.

Это, однако, не означает, что, если вы знаете сумму (в долларах), потраченную вами на рекламную кампанию, то вы сможете точно определить объёмы продаж. Например, подставьте в уравнение значение $55400 (сумма, потраченная на рекламу) вместо х, и получите ответ – 35302 единицы продукции. Обратите внимание, что значение $55400 приведено на рис. 1 в качестве одного из фактических результатов наблюдений, однако этому значению соответствует совсем другое значение объёма продаж – 9554. Итак, повторяю: на основе имеющихся у вас данных регрессия даёт наиболее точную оценку (35302 единицы), но не абсолютно точный прогноз.

Рассматривая принципы регрессионного анализа, очень важно понять, что регрессия выражает связь между переменными, а это не то же самое, что причинная обусловленность, означающая, что манипуляции с одной переменной неизбежно приведут к изменению другой.

Вы могли бы, например, подставить в уравнение регрессии значение $200000 и получить в качестве приблизительной оценки объёма продаж в единицах продукции 113818. Это вовсе не обязательно означает, что , потратив на рекламу $200000, вы продадите 113818 единиц этой продукции (хотя, конечно, это и не исключено). Существует множество факторов, кроме суммы расходов на рекламу, влияющих на изменения в объёмах продаж, и эти факторы (например, продажная цена единицы продукции) в уравнении регрессии никак не отражены.

Даже если связь между переменными носит причинный характер, вы ни коим образом не можете быть уверены в направлении этой причинности. Вполне вероятна ситуация, когда отдел маркетинга увеличит расходы на рекламу продукции после того, как увеличатся объёмы её продаж. В этом случае именно объёмы продаж будут влиять на размеры сметы на рекламу, а не наоборот.

Правая часть уравнения регрессии – число 0,543 – называется угловым коэффициентом, а число 5221,1 – отрезком, отсекаемым на оси ординат. Коэффициент наклона представляет собой меру наклона линии тренда: чем больше число, определяющее этот коэффициент, тем круче линия тренда. Коэффициент наклона может быть отрицательным числом; и в этом случае линия тренда будет идти из верхнего левого угла графика в нижний правый. Если вам, например, пришлось бы составить график соответствия цены единицы продукции объёмам продаж в единицах продукции, полученная линия тренда, вероятнее всего, имела бы отрицательный наклон: чем больше цена, тем меньше единиц продукции продаётся.

Отрезок на оси ординат указывает, в каком месте линия тренда пересекает ось y (вертикальную ось). В данном случае – это число 52221,1. Это означает следующее: ²Если мы потратим на рекламу данной продукции $0,то , по предварительным оценкам, мы продадим 5220 экземпляров.²

На графике также указано значение преобразованной модели регрессии R²(приближенная оценка её фактического значения). Оно выражает долю дисперсии в у (в данном примере – в расходах на рекламу в долларах).

Представим, что между расходами на рекламу (в долларах) и объёмами продаж (в единицах продукции) существует взаимосвязь (это необязательное предположение, но с его помощью легче понять суть дальнейшего изложения). Когда вы изменяете смету на рекламу продукции, объёмы её продаж также изменяются. Когда изменяются объёмы продаж данной продукции, изменяется дисперсия объёмов продаж всех видов продукции. Чтобы доказать это, введите какие-нибудь числа в рабочий лист Excel – скажем, в ячейки А1:А5. Затем в другую ячейку введите следующую формулу:

=ДИСП(А1:А5)

Теперь, когда вы изменили все числа в ячейках А1:А5, можно увидеть, что значение, возвращённое формулой, также изменилось.

Изменяя значения в А1:А5, вы оказываете влияние на их дисперсию. Знпачение R², показанное на рис.1, равно 0,7081. Оно означает, что приблизительно 71% меры изменчивости объёмов продаж в единицах продукции связан с мерой изменчивости расходов на рекламу в долларах.

Но почему R²? Потому что значение R² является квадратом коэффициента корреляции. Если бы вы ввели в рабочий лист, показанный на рис.1, следующую формулу:

=КОРРЕЛ(А3:А20; В3:В20)^2

она вернула бы число 0,7081, т.е. значение, совпадающее со значением R² для этих данных.

ЗАДАНИЕ

Построить регрессионную зависимость для следующих данных:

	x	z	y			функция
	2,5	7,1	2,5			y=f(x)
	3,4	5,4	6,3			z=f(x)
		8,7	7,8			x=f(y)
		4,5	9,3			x=f(z)
		3,2	10,8			y=f(z)
	2,3	5,6	12,3			z=f(y)
		8,1	13,8			y=f(x)
	4,5	9,4	15,3			z=f(x)
	3,2	10,7	7,1			x=f(y)
	5,6		5,4			x=f(z)
	8,1	13,3	8,7			y=f(z)
	9,4	14,6	3,2			z=f(y)
		2,5	9,1			y=f(x)
	5,4	3,4	8,5			z=f(x)
	2,1		4,7			x=f(y)
	8,4	8,7	7,8			x=f(z)
		4,5	9,3			y=f(z)
	7,1	3,2	10,8			z=f(y)
	5,4	5,6	12,3			y=f(x)
	8,7	8,1	13,8			z=f(x)
	3,2	9,4	15,3			x=f(y)
	9,1	10,7	16,8			x=f(z)
	8,5		18,3			y=f(z)
	4,7	13,3	19,8			z=f(y)
	0,9	14,6	21,3			y=f(x)