Собственные числа и собственные векторы матрицы линейного преобразования (оператора)

Всякий ненулевой вектор х(а₁,а₂,...,а_nназывается собственным вектором линейного преобразования, если

Ах=λx, (1.5.4) где λ -некоторое число, называемое собственным значением (числом) линейного преобразования.

Если матрица А имеет вид (1.5.2), то равенство (1.5.4) запи­сывается в виде системы линейных алгебраических уравнений (Дц - Л)а^ -ь a^a^+...+а^а^ = О

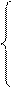(a₁₁- λ)a₁+a₁₂a₂+...+a_1na_n=0

a₂₁a₁+(a₂₂- λ)a₂+...+a_2na_n=0

----------------------------------- (1.5.5)

a_n1a₁+a_n2a₂+...+(a_nn- λ)a_n=0

Система (1.5.5), однородная СЛАУ, имеет отличные от нуля (нетривиальные) решения только тогда, когда определитель равен нулю. Отсюда следует, что

det(A- λE)=0. (1.5.6) Уравнение (1.5.6) называется характеристическим уравнением матрицы данного линейного преобразования. Каждый действительный корень λ уравнения (1.5.6) является собственным числом. Соответствующие собственному числу координаты собственного вектора находятся из системы (1.5.5) методом, изложенном в теме 1.1 (см. пример 1.1.11).

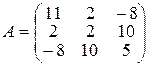Пример 1.5.4.Найти собственные числа и собственные векторы матрицы линейного преобразования.

Система однородных линейных алгебраических уравнений (1.5.5) для нахождения собственных векторов имеет вид:

(11-λ)а₁+2а₂-8а₃=0

2а₁+(2-λ)а₂+10а₃=0 (1.5.7)

-8а₁+10а₂+(5-λ)а₃=0

Вычислим определитель (1.5.6) и решим соответствующее характеристическое уравнение

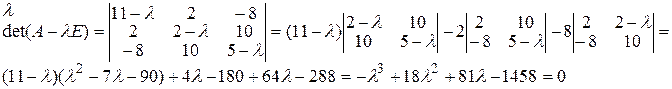
Характеристическое уравнение имеет вид

λ³-18 λ²-81 λ+1458=0, а его решение λ₁=9, λ₂=18, λ₃=-9. Найденные зна­чения λ_і, і=1,3 подставим в (1.5.7)

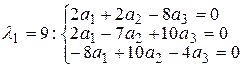
Решение этой системы х₁= С(2,2,1)^Т, С єR, а соответствующий еди­ничный вектор х⁰₁ =(2/3, 2/3, 1/3) ^Т

При λ ₂=18: х⁰₂=(-2/3, 1/3, 2/3)^Т при λ₃=-9 х⁰₃ =(1/3, -2/3, 2/3)

Решения систем линейных уравнений рассмотрены в теме 1.1 (см. пример 1.1.11).

Необходимо отметить следующие свойства собственных значений и собственных векторов симметрической матрицы.

1.Корни характеристического уравнения вещественной симметрической матрицы вещественны.

2.Собственные векторы вещественной симметрической матрицы, отве­чающие различным собственным значениям ортогональны. (Проверьте на собственных векторах матрицы примера 1.5.4).

Вопросы для самопроверки

1.Приведите примеры n-мерных векторов.

2.Что такое линейное векторное пространство, какое пространство

называется евклидовым?

З. Что такое базис в n -мерном пространстве?

4 . Как определяется линейное преобразование?

5.Докажите неравенство Коши-Буняковского.

6. Докажите неравенство ||x+y||≤||x||+||y||

7. При каком условии матрица линейного преобразования имеет диаго­нальный вид?

8.Сформулируйте алгоритм нахождения собственных векторов.

Тема 1. 6 . Квадратичные формы. Приведение к каноническому виду уравнений линии и поверхности второго по­рядка

Квадратичной формой от трех переменных x,y,z называется одно­родный многочлен второй степени относительно этих переменных.

F(x,y,z)= a₁₁x² + 2a₁₂xу+ а₂₂у² + 2a₁₃xz+ 2a₂₃yz+a₂₂ z² (1.6.1)

Если учесть, что а₁₂ =a₂₁, a₁₃=a₃₁, a₂₃=a₃₂ , тоF(x,y,z) записывается

в виде

F(x, у, z) = а₁₁х² + а₁₂ху + а₂₁ух + а₂₂ у² + a₁₃xz + a₃₁ zx + a₂₃ yz + a₃₂ zy + a₂₂z² .

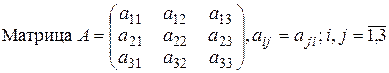
называется матрицей квадратичной формы. Квадратичная форма имеет канонический вид, если она содержит члены только с квадратами пе­ременных, т.е. а_ij = 0; i,j = 1,3; i≠ j . Матрица (1.6.2) квадратичной формы

(1.6.1) будет иметь диагональный вид, если в трехмерном про­странстве перейти к. новому базису, состоящему из собственных век­торов (см. тему 1.5) матрицы А, при этом на главной диагонали бу­дут стоять собственные числа матрицы А.

Квадратичная форма в новом базисе будет иметь вид

F(x₁, y_1, z₁)=λ₁x₁² + λ₂ y₁² + λ₃z₁² (1.6.3)

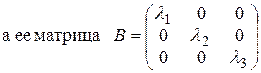
В случае двух переменных х, у квадратичная формаF(x,y) имеет вид

F(х,у) = а₁₁х² + 2а₁₂ ху + а₂₂ y², (1.6.4)

причем а₁₂ = a₂₁ .

Методы приведения квадратичной формы к каноническому виду применяются при решении задач на приведение к каноническому виду уравнений кривых второго порядка

a₁₁x² + 2а₁₂ ху + а₂₂ у² + b₁х + b₂ y + с = 0

и уравнений поверхностей второго порядка

a₁₁x² + 2а₁₂ ху + а₂₂ у² + 2a₁₃ xz+2a₂₃ yz+a₂₂ z² +b₁х + b₂ y +b₃ z + с = 0

Канонические уравнения основных кривых второго' порядка были рассмотрены в теме 1.4 (1.4.6). Поверхности второго порядка делятся на центральные и нецен­тральные. Канонические уравнения некоторых поверхностей второго порядка приведены ниже.