Есть ли «структура» у магнитного поля?
«Двуликая» природа ЭМИ тесно связана с представлениями о «структуре» магнитного поля. По мысли творцов электродинамики эта «структура» задается линиями поля. Объяснение явления ЭМИ «способом пересечения» предполагает у магнитного поля наличие такой структуры. «Теория взаимодействия полей» не нуждается в представлении магнитного поля «силовыми линиями». Поэтому сторонники этой теории считают магнитное поле бесструктурным. Одним из таких сторонников был академик И.Е. Тамм. Критикуя «механизм пересечения», он писал:
«… такая интерпретация не выдерживает никакой критики: силовые линии являются лишь вспомогательным понятием, … а не какими-либо материальными образованиями, отдельные элементы которых можно было бы индивидуализировать…»[4].
То есть, понимая, что магнитное поле – категория нематериальная, автор, тем не менее, не считает возможным мысленно наделить ее некоторой «структурой». (Между строк заметим, что эта точка зрения не помешала в свое время «материализовать» МП, присвоив ему массу, импульс и прочие свойства материального объекта!).
Мы показали, что разрешить некоторые «парадоксы» ЭМИ возможно лишь с помощью механизма пересечения, для которого структурированность магнитного поля – обязательное условие. Из-за того, что в электродинамике уже более 100 лет господствует "теория взаимодействия полей", долго не находили разрешения классические «парадоксы»– Геринга и Фарадея.
Все эти проблемы снимаются, если допустить, что магнитное поле имеет «структуру», а магнитные силы – это силы «натяжения и давления» силовых линий.
Магнитное поле в космосе
Одним из основных выводов из системы уравнений Максвелла является предсказание существования электромагнитных волн (ЭМВ) и его гениальная догадка, что свет имеет электромагнитную природу. Вместе со светом электромагнитные взаимодействия «вышли в космос». Новое «рабочее место» потребовало от магнитного поля новых «способностей».
Мы видели, что большинство «парадоксов» в электродинамике связано с идеей «взаимодействия полей». Альтернативой этой теории является «механизм пересечения», который предполагает участие заряженных частиц. Но СТО утверждает, что межзвездное пространство пусто! В космосе нет (ну – почти нет!) заряженных частиц. Как же электромагнитные волны могут распространяться в пустом пространстве? Как в пустоте образуется ток, создающий магнитное поле – магнитную составляющую электромагнитных волн? И как в вакууме работает «механизм пересечения», генерирующий электрическую компоненту ЭМВ?
Стоит лишь удивляться (восторгаться!) изобретательности теоретиков, которые, пренебрегая законами природы и здравым смыслом, все-таки «решили» все эти проблемы. Но это – отдельный разговор. Об истории этих «изысканий», о новых свойствах, которыми наделили магнитное (и электрическое) поле теоретики и о новых «парадоксах», к которым привели эти разработки, мы расскажем позже. А пока обратимся к электрическому полю.
Единицы измерения
Величина B в системе единиц СИ измеряется в теслах, в системе СГС в гауссах.
Векторное поле H измеряется в амперах на метр (А/м) в системе СИ и в эрстедах в СГС. Эрстеды и гауссы являются тождественными величинами, их разделение является чисто терминологическим.
Приращение плотности энергии магнитного поля равно:
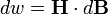
где:
H — напряжённость магнитного поля,
B — магнитная индукция
В линейном тензорном приближении магнитная проницаемость есть тензор (обозначим его 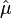 ) и умножение вектора на неё есть тензорное (матричное) умножение:
) и умножение вектора на неё есть тензорное (матричное) умножение:
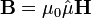 или в компонентах[12]
или в компонентах[12] 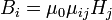 .
.
Плотность энергии в этом приближении равна:
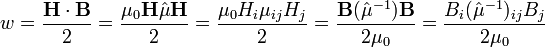
где:
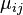 — компоненты тензора магнитной проницаемости,
— компоненты тензора магнитной проницаемости,
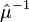 — тензор, представимый матрицей, обратной матрице тензора магнитной проницаемости,
— тензор, представимый матрицей, обратной матрице тензора магнитной проницаемости,
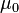 — магнитная постоянная
— магнитная постоянная
При выборе осей координат совпадающими с главными осями[13] тензора магнитной проницаемости формулы в компонентах упрощаются:
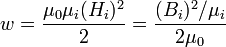
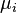 — диагональные компоненты тензора магнитной проницаемости в его собственных осях (остальные компоненты в данных специальных координатах — и только в них! — равны нулю).
— диагональные компоненты тензора магнитной проницаемости в его собственных осях (остальные компоненты в данных специальных координатах — и только в них! — равны нулю).
В изотропном линейном магнетике:
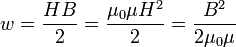
где:
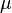 — относительная магнитная проницаемость
— относительная магнитная проницаемость
В вакууме 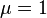 и:
и:
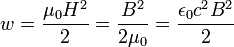
Энергию магнитного поля в катушке индуктивности можно найти по формуле:
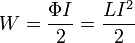
где:
Ф — магнитный поток,
I — ток,L — индуктивность катушки или витка с током.
