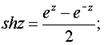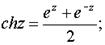Понятие функции комплексного переменного
Понятие функции комплексного переменного является частным случаем общего математического понятия функции.
Определение. Если А – некоторое множество комплексных чисел z (геометрически – множество точек комплексной плоскости), и каждому числу z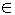 
А поставлено в соответствие по некоторому закону число w 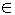В (где В – также множество комплексных чисел), то говорят, что на множестве А определена функция комплексного переменного z (или отображение множества А в В ).
Записывают: w = f (z).
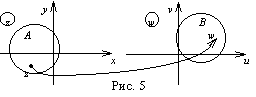Множество А называют областью определения функции, В – множество, состоящее из значений, принимаемых функцией, называют областью значений функции.
Принято множества А и В, изображать на отдельных комплексных плоскостях (см. рис. 5): плоскость z комплексных чисел z = х + i у и плоскость w комплексных чисел w = u + i v .
При этом точка w0 = f (z0) называется образом точки z0, а z0– прообразом точки w0.
В частности, если А расположено на действительной оси ох, то z = х является действительным переменным. Если же все значения w также действительны, то приходим к понятию функции действительного переменного как частному случаю функции комплексного переменного.
В общем случае z = х + i у, w = u (х, у) + i v (х, у).
Геометрически функцию f (z ) можно рассматривать как отображение множества А на множество В, переводящее точку (х, у) множества А в точку ( u, v ) множества В. Высказывание “ функция w = f (z) определена на множестве А”эквивалентно следующему: “ каждой точке (х, у) из А поставлены в соответствие действительные числа u и v ” . Иными словами, на множестве А определены две действительные функци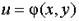и
и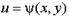 
двух действительных переменных х и у. Итак, задание функции комплексного переменного w = f (z) равносильно заданию двух функций двух действительных переменных 
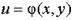и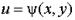 
.
Например, соотношение w = z2 = (x +iy)2 = x2 – y2 + i2xy эквивалентно следующим: u = x2 – y2, v = 2xy.
Пример 1. Дана функция f (z) = z3 + i . Найти мнимую и действительную части этой функции.
Решение. f (z) = (х + i у)3 + i = x3 + 3x2iy + 3x(iy)2 + (iy)3 + i = x3 – 3xy2 + i (3x2y – y3 + 1).
Откуда u(x,y) = x3 – 3xy2 , v(x,y) = 3x2y – y3 + 1.
Замечание.
.
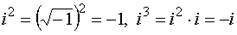ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Следующие функции (как однозначные, так и многозначные) называют основными элементарными функциями:
Дробно-рациональная функция
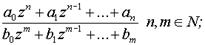
2. Показательная функция:
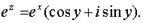
Наряду с введенным обозначением для показательной функции используют обозначение exp z.
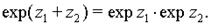
Показательная функция комплексного переменного является периодической функцией с основным периодом 2pi, т. е.
.
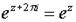3. Тригонометрические функции:
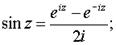
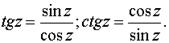
4. Гиперболические функции:
