Сходимость произвольных рядов
Ряды, в которых имеется бесконечное количество положительных членов и бесконечное количество отрицательных членов называют знакопеременными.
Ряды знакочередующиеся: 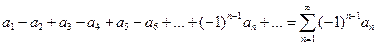 . Здесь полагаем все
. Здесь полагаем все 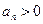 . В таком ряде знаки + и - чередуются и идут через один, откуда и название ряда.
. В таком ряде знаки + и - чередуются и идут через один, откуда и название ряда. 
Признак Лейбница. Если члены ряда 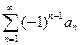 :
: 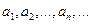 монотонно убывают:
монотонно убывают: 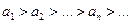 и если общий член
и если общий член 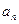 стремится к нулю (
стремится к нулю ( 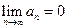 ), то ряд
), то ряд 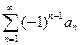 сходится.Cходящийся ряд называют рядом лейбницевского типа.
сходится.Cходящийся ряд называют рядом лейбницевского типа.
Для доказательства сначала рассмотрим частичные суммы с четными номерами: 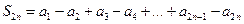 . Объединяем слагаемые в этой сумме:
. Объединяем слагаемые в этой сумме: 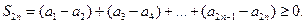 Таким образом,
Таким образом, 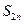 равна сумме положительных слагаемых и следовательно, не убывает, является монотонно возрастающей последовательностью. Она ограничена сверху:
равна сумме положительных слагаемых и следовательно, не убывает, является монотонно возрастающей последовательностью. Она ограничена сверху: 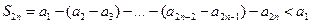 . Итак,
. Итак, 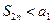 - последовательность ограничена сверху. Она имеет предел:
- последовательность ограничена сверху. Она имеет предел: 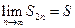 . Но если перейти к суммам нечетным, то будем иметь:
. Но если перейти к суммам нечетным, то будем иметь: 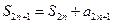 . Поскольку предел
. Поскольку предел 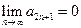 , то имеем окончательно:
, то имеем окончательно: 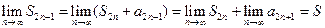 . Другими словами, четные и нечетные частичные суммы имеют один и тот же предел. Отсюда заключаем, что ряд сходится. Попутно мы доказали, что
. Другими словами, четные и нечетные частичные суммы имеют один и тот же предел. Отсюда заключаем, что ряд сходится. Попутно мы доказали, что 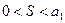 .
.
На основании этого неравенства удобно оценивать сумму остатков 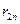 и
и 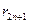 . Имеем:
. Имеем: 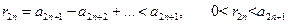
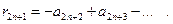 Ясно, что
Ясно, что 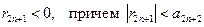 . Объединяя неравенства для
. Объединяя неравенства для 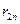 и
и 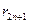 , можно написать
, можно написать 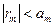 , где m – произвольное натуральное число, четное или нечетное. Таким образом, при замене суммы знакочередующегося ряда Лейбница на его частичную сумму мы совершаем ошибку, не превосходящую (по модулю) первого отброшенного члена рядя.
, где m – произвольное натуральное число, четное или нечетное. Таким образом, при замене суммы знакочередующегося ряда Лейбница на его частичную сумму мы совершаем ошибку, не превосходящую (по модулю) первого отброшенного члена рядя.
Пример: 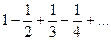 - ряд сходится по признаку Лейбница, ибо
- ряд сходится по признаку Лейбница, ибо 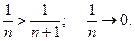 Это ряд Лейбница. Позже будет показано, что
Это ряд Лейбница. Позже будет показано, что 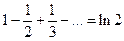 .
.
Требование монотонности стремления членов знакочередующегося ряда к нулю существенное для его сходимости. Если оно не выполнено, то возможна расходимость ряда, несмотря на стремление к нулю его членов. В качестве примера такого поведения рассмотрим ряд: 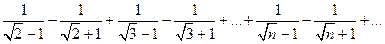 . Члены этого ряда не удовлетворяют условию монотонности стремления к нулю :
. Члены этого ряда не удовлетворяют условию монотонности стремления к нулю : 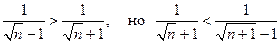 . Для него имеем:
. Для него имеем: 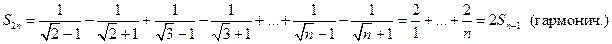
Но гармонический ряд расходится, поэтому рассмотренный знакочередующийся ряд также расходится.
Заметим, что в теореме Лейбница условия монотонности можно ослабить. Достаточно потребовать монотонности членов ряда, начиная с некоторого места (номера n). Т.е. первые члены знакочередующегося ряда могут не удовлетворять условию монотонности.
Поэтому если рассмотреть ряд 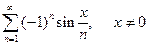 , то увидим, что при любом фиксированном x , для достаточно больших n ,
, то увидим, что при любом фиксированном x , для достаточно больших n , 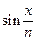 имеет один определенный знак, и имеем ослабление условий, ряд сходится при любом x.
имеет один определенный знак, и имеем ослабление условий, ряд сходится при любом x.
Определение функционального ряда. Точка сходимости функционального ряда, точка расходимости. Определение области сходимости и области расходимости функционального ряда. Примеры нахождения области сходимости и области расходимости рядов.
Функциональные ряды
Ряды, членами которых являются не числа, а функции от некоторого аргумента x,а именно,
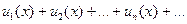 , называют функциональным. Предполагается, что функции
, называют функциональным. Предполагается, что функции 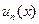 определены на одной и той же области определения.
определены на одной и той же области определения.
Ряд 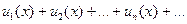 может при одних x сходиться, а при других x - расходиться.
может при одних x сходиться, а при других x - расходиться.
Если при некотором x=x0 ряд сходится, то такую точку называют точкой сходимости ряда. Совокупность (множество) точек сходимости образует область сходимости ряда. Итак, область U является областью сходимости, если в каждой точке U ряд 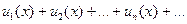 сходится.
сходится.
Пример. Функциональный ряд: 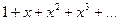
сходится в области 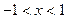 . При
. При 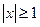 этот ряд расходится.
этот ряд расходится.
Для сходящегося ряда 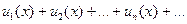 определена сумма S. Очевидно, она будет также зависеть от x, т.е. S=S(x):
определена сумма S. Очевидно, она будет также зависеть от x, т.е. S=S(x): 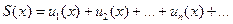 в области сходимости.
в области сходимости.
Заметим, что S(x) может оказаться определенной не только в области сходимости ряда, но и в более широкой области. Например:
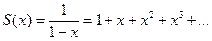 определена при любом
определена при любом 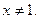
В общем случае S(x) определяется через частичные суммы 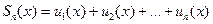 . Имеем по определению
. Имеем по определению 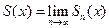 в точке сходимости. Также в точке сходимости имеем для остатка
в точке сходимости. Также в точке сходимости имеем для остатка
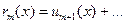 свойство
свойство 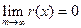 .
.
Изучение свойств функционального ряда сводится, в общем случае, к решению вопроса: заданы свойства членов ряда 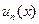 . Какими будут свойства суммы?
. Какими будут свойства суммы?
Например, пусть в области сходимости U члены ряда 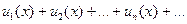 являются непрерывными функциями. Можно ли гарантировать, что и сумма S(x) будет непрерывной в U функцией? Напомним, что если в конечной сумме
являются непрерывными функциями. Можно ли гарантировать, что и сумма S(x) будет непрерывной в U функцией? Напомним, что если в конечной сумме 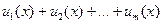 слагаемые – непрерывные функции, то и сумма будет непрерывной. Возникает вопрос: переносится ли это свойство безоговорочно и на бесконечные суммы (ряды)? Примеры показывают, что нет.
слагаемые – непрерывные функции, то и сумма будет непрерывной. Возникает вопрос: переносится ли это свойство безоговорочно и на бесконечные суммы (ряды)? Примеры показывают, что нет.
Рассмотрим ряд
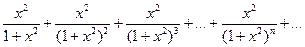
При x=0 ряд сходится и имеет суммой 0: S(0)=0. При x¹0 имеем геометрическую прогрессию, сумма S(x) которой равна:
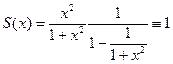
Итак, S(0)=0, S(x)=1. Сумма S(x) оказалась разрывной. Но все члены ряда 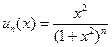
- непрерывные функции!
Итак, одной непрерывности членов ряда недостаточно для того, чтобы сумма ряда была определенной и непрерывной – как видим, она может быть разрывной.
Дополнительным условием, обеспечивающим непрерывность суммы, будет так называемое условие равномерной сходимости ряда.
Определение. Ряд 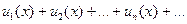 равномерно сходится в некоторой области D, если для произвольного e > 0 найдется такой номер N, зависящий от e (N = N(e)), что выполняется неравенство
равномерно сходится в некоторой области D, если для произвольного e > 0 найдется такой номер N, зависящий от e (N = N(e)), что выполняется неравенство 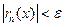 для всех xÎD и для любого n>N(e). Может случиться, что во всех точках области D ряд
для всех xÎD и для любого n>N(e). Может случиться, что во всех точках области D ряд 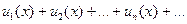 сходится, но остаток ряда не удовлетворяет написанному выше условию равномерной сходимости. Рассмотрим предыдущий пример. При x=0, rn(0)=0; при x¹0 имеем
сходится, но остаток ряда не удовлетворяет написанному выше условию равномерной сходимости. Рассмотрим предыдущий пример. При x=0, rn(0)=0; при x¹0 имеем
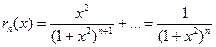
Все rn(x) при x ®0 стремятся к 1, и условие 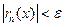 не может быть удовлетворено, если e <1.
не может быть удовлетворено, если e <1.
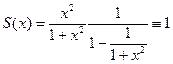
Итак, S(0)=0, S(x)=1. Сумма S(x) оказалась разрывной. Но все члены ряда 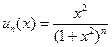
- непрерывные функции!
Итак, одной непрерывности членов ряда недостаточно для того, чтобы сумма ряда была определенной и непрерывной – как видим, она может быть разрывной.
Дополнительным условием, обеспечивающим непрерывность суммы, будет так называемое условие равномерной сходимости ряда.
Определение. Ряд 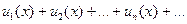 равномерно сходится в некоторой области D, если для произвольного e > 0 найдется такой номер N, зависящий от e (N = N(e)), что выполняется неравенство
равномерно сходится в некоторой области D, если для произвольного e > 0 найдется такой номер N, зависящий от e (N = N(e)), что выполняется неравенство 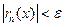 для всех xÎD и для любого n>N(e). Может случиться, что во всех точках области D ряд
для всех xÎD и для любого n>N(e). Может случиться, что во всех точках области D ряд 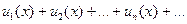 сходится, но остаток ряда не удовлетворяет написанному выше условию равномерной сходимости.
сходится, но остаток ряда не удовлетворяет написанному выше условию равномерной сходимости.
Рассмотрим предыдущий пример. При x=0, rn(0)=0; при x¹0 имеем
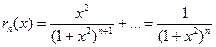 , Все rn(x) при x ®0 стремятся к 1, и условие
, Все rn(x) при x ®0 стремятся к 1, и условие 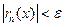 не может быть удовлетворено, если e <1.
не может быть удовлетворено, если e <1.
42.Определение равномерной сходимости ряда в некоторой области. Признак Вейерштрасса равномерной сходимости.
Достаточным признакомравномерной сходимости будет признак Вейерштрасса:
Ряд 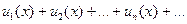 равномерно сходится в области D, если существует некоторый положительный сходящийся числовой ряд
равномерно сходится в области D, если существует некоторый положительный сходящийся числовой ряд 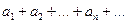 , для которого во всей области D выполняются неравенства:
, для которого во всей области D выполняются неравенства: 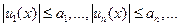 .
.
Действительно, имеем: 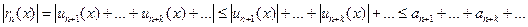
Но ряд 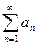 сходится, и его остаток
сходится, и его остаток 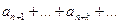 стремится к нулю при n®¥, и следовательно для любого e>0 найдется такое N, что для любого n>N ,
стремится к нулю при n®¥, и следовательно для любого e>0 найдется такое N, что для любого n>N , 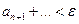 . Тогда
. Тогда 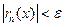 при любом n >N, что и требовалось. Мы видели, что ряд
при любом n >N, что и требовалось. Мы видели, что ряд 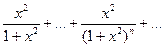 сходится всюду на оси x, но неравномерно. Любопытно отметить, что ряды
сходится всюду на оси x, но неравномерно. Любопытно отметить, что ряды 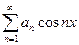 и
и 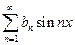 сходятся равномерно, если сходятся ряды
сходятся равномерно, если сходятся ряды 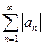 и
и 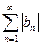 .Дадим еще примерравномерно сходящегося ряда:
.Дадим еще примерравномерно сходящегося ряда: 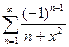 . Можно видеть, что при любом значении аргумента x этот ряд будет знакочередующимся. Следовательно, для его остатка имеем оценку:
. Можно видеть, что при любом значении аргумента x этот ряд будет знакочередующимся. Следовательно, для его остатка имеем оценку:
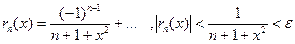
Следовательно, ряд сходится равномерно на всей числовой оси x .Из признака Вейерштрасса следует, что если к ряду 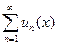 применим этот принцип, то и ряд
применим этот принцип, то и ряд 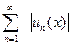 будет равномерно сходящимся в области D. Однако возможны случаи, когда ряд
будет равномерно сходящимся в области D. Однако возможны случаи, когда ряд 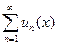 равномерно сходится, но ряд
равномерно сходится, но ряд 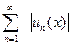 даже расходится. Примером может служить ряд
даже расходится. Примером может служить ряд 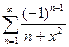 , который сходится равномерно на всей числовой оси x , но ряд
, который сходится равномерно на всей числовой оси x , но ряд 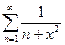 расходится при любом x.
расходится при любом x.
Это говорит о том, что к некоторым рядам невозможно «подойти» с помощью признака Вейерштрасса. Чтобы как-то отделить, уточнить характер равномерно сходящихся (по определению) рядов от рядов, равномерную сходимость которых можно определить по признаку Вейерштрасса, говорят, что если ряд удовлетворяет признаку Вейерштрасса, то он сходится правильно. Правильная сходимость – это, описательно говоря, равномерная сходимость высшей категории.
Основные аналитические свойства функциональных рядов: при каких условиях возможен почленный переход к пределу в ряде, условие непрерывности суммы ряда. Сформулировать условия, при которых возможно почленное интегрирование ряда, почленное дифференцирование ряда.
Свойства:
1. Непрерывность суммы равномерно сходящегося ряда.
Пусть ряд 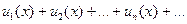 равномерно сходится в некоторой области D, причем его члены
равномерно сходится в некоторой области D, причем его члены 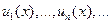 являются непрерывными в D функциями. Тогда и сумма ряд S(x) будет непрерывной функцией в области D.
являются непрерывными в D функциями. Тогда и сумма ряд S(x) будет непрерывной функцией в области D.
Для доказательства обозначим S n(x) частичную сумму ряда и пусть rn(x) - остаток ряда. Имеем по определению: 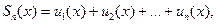
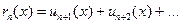 .
.
Тогда 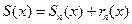 . Берем произвольную точку x0 ÎD . Рассмотрим
. Берем произвольную точку x0 ÎD . Рассмотрим 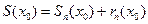 и составим приращение суммы ряда в точке x0 :
и составим приращение суммы ряда в точке x0 : 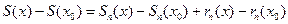 . Далее, для модулей:
. Далее, для модулей:
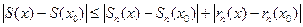 . Берем произвольное e>0 . Подберем такое N, чтобы для всех n>N имели место неравенства:
. Берем произвольное e>0 . Подберем такое N, чтобы для всех n>N имели место неравенства: 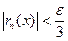 и
и 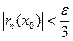
Тогда в D имеем: 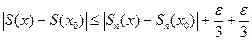 . Зафиксируем n и учтем при этом, что Sn(x) - непрерывная функция в точке x0 . Тогда можно подобрать x , близкое к x0 , чтобы
. Зафиксируем n и учтем при этом, что Sn(x) - непрерывная функция в точке x0 . Тогда можно подобрать x , близкое к x0 , чтобы 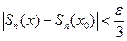 . В итоге имеем неравенство
. В итоге имеем неравенство 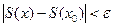 , означающее в силу произвольности e непрерывность суммы ряда в произвольной точке x0 области D, то есть и во всей области D.
, означающее в силу произвольности e непрерывность суммы ряда в произвольной точке x0 области D, то есть и во всей области D.
2. Почленный переход к пределу.
Пусть в области D ряд 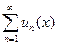 сходится равномерно и его сумма равна S(x). Пусть существуют пределы
сходится равномерно и его сумма равна S(x). Пусть существуют пределы 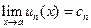 , где a - точка области D. Тогда существует предел
, где a - точка области D. Тогда существует предел 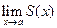 , причем
, причем 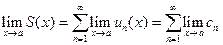 (без доказательства).
(без доказательства).
3. Почленное интегрирование ряда .
Теорема. Если ряд 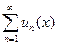 из непрерывных функций un(x) сходится в области D : a £ x £ b равномерно, то сумму ряда S(x) можно интегрировать, причем
из непрерывных функций un(x) сходится в области D : a £ x £ b равномерно, то сумму ряда S(x) можно интегрировать, причем
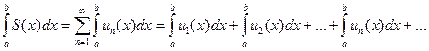
Таким образом, равномерно сходящийся ряд можно почленно интегрировать, причем проинтегрированный ряд будет сходиться. Имеем:
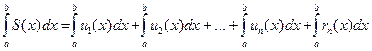
Берем "e>0. Докажем, что можно удовлетворить неравенству 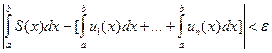
подбирая n большим. В силу равномерной сходимости ряда на отрезке a £ x £ b можно утверждать, что существует такое натуральное N , что при всех n >N , 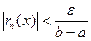 . Тогда:
. Тогда: 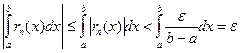 , что и требовалось.
, что и требовалось.
Итак, для равномерно сходящегося ряда имеем: 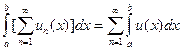 .
.
4. Теорема о дифференцировании ряда.
Пусть ряд 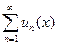 сходится к S(x) равномерно в области D : [ a, b ] и пусть функции
сходится к S(x) равномерно в области D : [ a, b ] и пусть функции 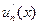 (все, при любом n) непрерывны в этой области. Тогда если ряд
(все, при любом n) непрерывны в этой области. Тогда если ряд 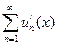 сходится равномерно в этой же области D , то его сумма равна
сходится равномерно в этой же области D , то его сумма равна 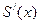 . По-другому, имеет место равенство:
. По-другому, имеет место равенство:
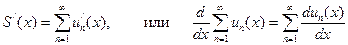
Действительно, если ряд 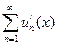 равномерно сходится в области [ a, b ], то можно взять произвольную точку x из этого отрезка, и если в этой точке имеет место равенство
равномерно сходится в области [ a, b ], то можно взять произвольную точку x из этого отрезка, и если в этой точке имеет место равенство 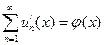 , то прежде всего будем иметь в виду, что j(x) непрерывна. Но тогда:
, то прежде всего будем иметь в виду, что j(x) непрерывна. Но тогда: 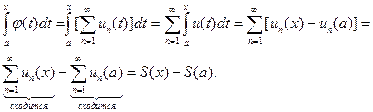
Следовательно, 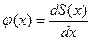 , что и требовалось доказать.
, что и требовалось доказать.
