Интегральная функция распределения F(х) и ее свойства
Функция распределения случайной величины X определяется по формуле
F(x)=P (X <x) . Это неубывающая функция, принимающая значения от 0 до 1. Если задана плотность распределения f(x)? то функция распределения выражается как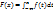 
26. Дифференциальная функция распределения £(х) и ее свойства.
Плотность распределения случайной величины X определяется по формуле
f (x)= F '(x) . Существует только для непрерывной случайной величины. Для нее выполняет ся условие нормировки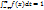 
(площадь под кривой равна 1)
Непрерывные случайные величины. Математическое ожидание непрерывной случайной величины и его свойства.
Непрерывной называют случайную величину, которая может принимать любые значения из некоторого заданного интервала, например, время ожидания транспорта, температура воздуха в каком-либо месяце, отклонение фактического размера детали от номинального, и т.д. Интервал, на котором она задана, может быть бесконечным в одну или обе стороны.
Математическое ожидание: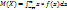 
Дисперсия, среднее квадратическсе отклонение непрерывной случайной величины и его свойства.
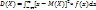или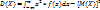 
Среднее квадратическое отклонение непрерывной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии: σ(X) = √D(X)
Мода непрерывной случайной величины Mo(X) - значение с.в., имеющее наибольшую вероятность. Если в задаче требуется определить моду - находим экстремум (максимум) плотности вероятности f(x).
Кривая Гаусса.
Симметричная параболическая кривая, иногда возникающая при изображении серии результатов на частотном графике. Многие переменные образуют нормальное распределение, когда измерения проводятся в целой популяции. Считается, что рост человека и коэффициент умственного развития подчиняются принципу нормального распределения при достаточно большом количестве участников. На кривой Гаусса большинство результатов концентр. вокруг центра, а наиболее высокие и низкие результаты встречаются гораздо реже. Эти «хвосты» нормального распределения вытягиваются в обоих направлениях вдоль оси абсцисс и теоретически никогда не соприкасаются с нею.
31. Мода и медиана нормального распределения.
для нормального распределения мода, медиана и среднее значение совпадают.
Мода непрерывной случайной величины Mo(X) - значение с.в., имеющее наибольшую вероятность. Если в задаче требуется определить моду - находим экстремум (максимум) плотности вероятности f(x).