Понятие степенного ряда

Важнейшие для практики функциональные ряды – это степенные ряды.

Степенным рядом называется функциональный ряд вида

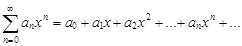, (11)

где числа а₀, а₁, а₂, ¼ – коэффициенты ряда;

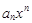– общий член степенного ряда (a_n ¹ 0).

Данный ряд называется степенным потому, что членами ряда служат степенные функции, показателями степеней которых являются целые неотрицательные числа.

Степенной ряд всегда сходится при х = 0.

Теорема Абеля. Если ряд (11) сходится при х = х₀ (х₀ ¹ 0), то он сходится абсолютно при любых значениях, для которых выполняется неравенство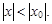

Если ряд (11) расходится при 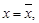то он расходится при любых значениях х, для которых выполняется неравенство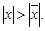

Областью сходимости степенного ряда называется совокупность тех значений х, при которых степенной ряд сходится.

Число R – такое, что при 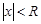ряд сходится, а при 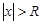– расходится, называется радиусом сходимости степенного ряда.

Интервал (–R; R) называется интервалом сходимости степенного ряда. При x = –R, x = R ряд может как сходится, так и расходится.

Радиус сходимости степенного ряда может быть найден по формуле

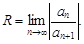(12)

Пример 15. Найти радиус, интервал, область сходимости степенного ряда .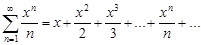

Решение

1. n-й член данного степенного ряда равен 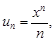n + 1-й член данного степенного ряда равен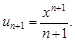

Коэффициенты при n-м и n+1-м членах ряда соответственно равны 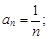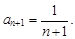По формуле (12) находим радиус сходимости

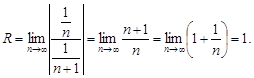
Таким образом, радиус сходимости: R = 1.

2. Интервал сходимости будет иметь вид (–1; 1).

3. Найдем область сходимости, для этого исследуем сходимость ряда на концах интервала сходимости: при x = –1 и x = 1.

При x = –1 получим числовой ряд с общим членом 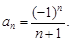Это знакочередующийся ряд. Для его сходимости применим признак Лейбница: если n = 1, то 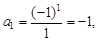если n = 2, то 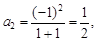если n = 3, то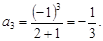

Члены данного числового ряда убывают по абсолютной величине

,

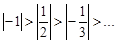следовательно, первое условие признака Лейбница выполняется.

Проверим выполнение второго условия признака Лейбница

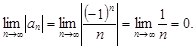
Общий член с возрастанием номера n стремится к нулю, следовательно, второе условие признака Лейбница выполняется.

Таким образом, согласно признаку Лейбница ряд сходится и значение x = –1 надо включить в интервал сходимости.

При x = 1 получим числовой ряд с общим членом 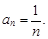Это гармонический ряд, который расходится. Следовательно, значение x = 1 не включаем в интервал сходимости.

Таким образом, область сходимости данного степенного ряда имеет вид [–1; 1).

Тест 15. Степенной ряд задан формулой общего члена 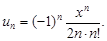Коэффициент при n-м члене равен:

1)

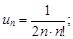
2)

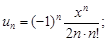
3)

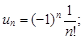
4)

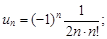
5)

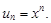
Тест 16.При x = 0 степенной ряд 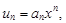a_n ¹ 0:

1) сходится;

2) расходится;

3) вопрос о сходимости ряда остается открытым.

Тест 17.Если ряд 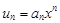сходится при 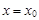( 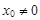), то он сходится абсолютно при любых значениях x, для которых выполняется неравенство:

1)

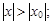
2)

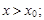
3)

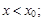
4)

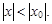
Тест 18.Если ряд 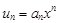расходится при 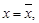то он расходится при любых значениях x, для которых выполняется неравенство:

1)

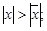
2)

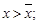
3)

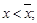
4)

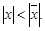
Тест 19.Радиус сходимости степенного ряда 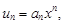a_n ¹ 0, вычисляется по формуле:

1)

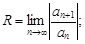
2)

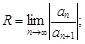
3)

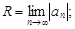
4)

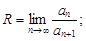
5)

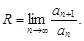
Тест 20.Степенной ряд задан формулой общего члена 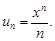Радиус сходимости данного ряда равен:

1)

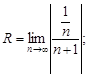
2)

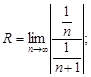
3)

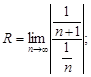
4)

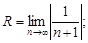
5)

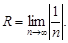
Тест 21.Радиус сходимости некоторого степенного ряда равен
R = 5, тогда интервал сходимости имеет вид:

1) (–5; 5);

2) (–5; 0);

3) (5; 0);

4) (–5; 0) È (0; 5);

5) (–¥; 0) È (5; ¥).

Тест 22.Интервал сходимости некоторого степенного ряда имеет вид (–5; 5). Причем, при x = –5 соответствующий числовой ряд сходится, а при x = 5 – расходится. Тогда область сходимости имеет вид:

1) (–5; 5);

2) [–5; 5);

3) [–5; 5];

4) (–5; 5];

5) (–¥; –5).

Тест 23.Интервал сходимости некоторого степенного ряда имеет вид (–5; 5). Причем, при х = –5 соответствующий числовой ряд расходится, а при х = 5 – сходится. Тогда область сходимости имеет вид:

1) (–5; 5);

2) [–5; 5);

3) [–5; 5];

4) (–5; 5];

5) (–¥; –5).

Тест 24.Интервал сходимости некоторого степенного ряда имеет вид (–5; 5). Причем, при х = –5 и х = 5 соответствующие числовые ряды сходятся. Тогда область сходимости имеет вид:

1) (–5; 5);

2) [–5; 5);

3) [–5; 5];

4) (–5; 5];

5) (–¥; –5).

Тест 25.Интервал сходимости некоторого степенного ряда имеет вид (–5; 5). Причем, при х = –5 и х = 5 соответствующие числовые ряды расходятся. Тогда область сходимости имеет вид:

1) (–5; 5);

2) [–5; 5);

3) [–5; 5];

4) (–5; 5];

5) (–¥; –5).

Пример 16.Найти область сходимости степенного ряда

.

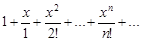Решение

Общий член данного ряда равен 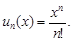Коэффициенты при n-м и n +1-м членах ряда соответственно равны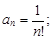 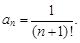По формуле (12) находим радиус

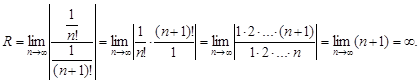
Таким образом, радиус сходимости: R = ¥.

Интервал сходимости: (–¥; ¥).

Следовательно, ряд сходится на всей числовой оси.

Пример 17.Найти область сходимости степенного ряда

.

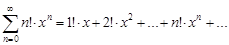Решение

Общий член данного ряда равен 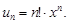Коэффициенты при n-м и n +1-м членах ряда соответственно равны a_n = n!; a_n = (n + 1)!. По формуле (12) находим радиус

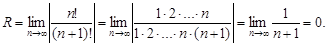
Таким образом, радиус сходимости: R = 0.

Следовательно, ряд сходится только в одной точке x = 0.

Тест 26.Радиус сходимости степенного ряда 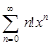равен R = 0. Тогда ряд сходится:

1) при х Î (–¥; +¥);

2) при х = 1;

3) при х Î (0; +¥);

4) только при х = 0;

5) при х Î (–¥; 0).

Тест 27.Радиус сходимости некоторого степенного ряда равен
R = ¥. Тогда ряд сходится:

1) при х Î (–¥; +¥);

2) при x = 1;

3) при х Î (0; +¥);

4) при x = 0;

5) при х Î (–¥; 0).