Расчет переходных процессов TRANSIENT

После перехода в режим анализа переходных процессов программа МС9 проверяет правильность составления схемы. При отсутствии ошибок в схеме программа открывает окно задания параметров моделирования Transient Analysis Limits (рисунок 5.14). Некоторые команды этого окна имеют тоже назначение, что и в окне DC анализа. Отметим особенности.

Time Range — конечное и начальное время расчета переходных процессов по формату Tmax[,Tmin]; по умолчанию назначается Tmin=0.

Maximum Time Step — максимальный шаг интегрирования. Расчет переходных процессов ведется с переменных шагом, выбираемым автоматически, величина которого определяется допустимой относительной ошибкой RELTOL.

Number of Points — количество точек, выводимых в таблицы, т. е. количество строк в таблице вывода результатов по умолчанию принимается равным 51. Если заданные моменты времени не совпадают со значениями, при которых проводился численный расчет, то производится интерполяция.

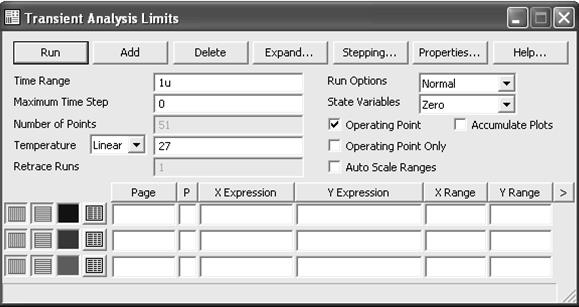
Рисунок 5.14 – Окно задания параметров анализа переходных процессов

Transient Analysis Limits

Stepping — открытие диалогового окна задания вариации параметров.

Properties — открытие диалогового окна, имеющего 5 или 6 закладок для управления выводом графиков, выбора масштабов по осям координат, выбора цвета объектов, параметров шрифта и типа линий, нанесения заголовков в выходных данных и т.д.

State Variables — установка начальных условий.

Operation Point — выполнение расчета режима по постоянному току перед началом каждого расчета переходных процессов. Данные этого режима заменяют значения всех начальных условий, если они были установлены.

Operation Point Only — расчет только режима по постоянному току.

Auto Scale Ranges — присвоение признака автоматического масштабирования «Auto» по осям X для каждого нового варианта расчетов.

X Expression— имя переменной, откладываемой по оси X. Обычно при анализе переходных процессов по этой оси откладывается время (переменная Т), однако это не всегда так. Так при расчете спектра сигнала с помощью преобразования Фурье (FFT) по оси X откладывается частота F,), а при расчете петли гистерезиса ферромагнетика — напряженность магнитного поля, например Н(К1).

Y Expression — математическое выражение для переменной, откладываемой по оси Y. Это может быть простая переменная типа напряжения в узле V(5), падения напряжения на двухполюсном компоненте V(L1), тока ветви I(2,3), I(L1) или математическое выражение, например V(VCC)*I(VCC). После щелчка правой кнопки мыши при расположении курсора в любой графе Y Expression открывается всплывающее меню, позволяющее выбрать из предлагаемых списков переменные и константы, размещаемые в этих графах.

Иконка на панели инструментов открывает режим анимации (Animate), который позволяет замедлить вывод графиков, что удобно при построении наряду с зависимостями во времени зависимостей различных величин между собой.

После перехода в режим расчета переходных процессов в составе меню команд появляются новы команды, в частности, следующие.

Limits — вызов окна задания параметров моделирования и построения графиков.

Stepping — вызов окна многовариантного анализа.

Optimize — вызов окна параметрической оптимизации.

Analysis Window (F4) — открытие графического окна результатов моделирования;

3D Windows — добавление/удаление окна трехмерной графики.

State Variables Editor — вызов редактора значений переменных состояния. В появившемся окне в трех колонках располагаются значения узловых потенциалов Node Voltages, токов через катушки индуктивностей Inductor Currents и логических состояний цифровых узлов Node Levels.

Пример.

Рассчитаем реакцию простейших интегрирующей (удлиняющей) и дифференцирующей (укорачивающей) цепей на входное воздействие в виде прямоугольных импульсов (рисунок 5.15).

Здесь же продемонстрирован режим пошагового анализа Stepping: величины резисторов R1 и R2 изменяются в заданных пределах, тем самым изменяя постоянные времени цепей. В соответствии с этим, изменяется и скорость изменения кривых напряжения на выводах цепей. Для подписи значений изменяемых параметров использована команда ниспадающего меню Scope > Label Branches.

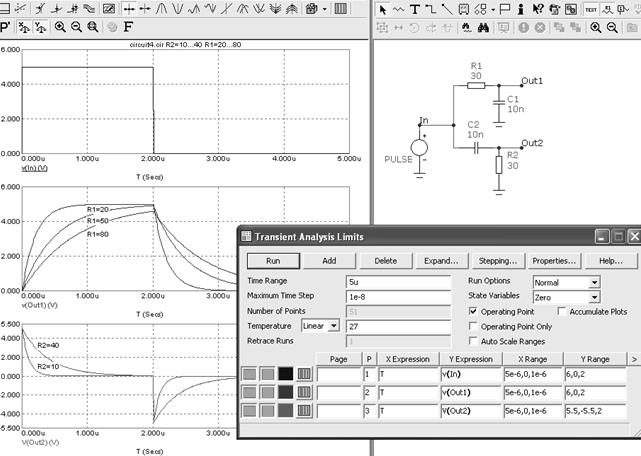
Рисунок 5.15 – Временные диаграммы работы простейших цепей.

Пример.

Смоделируем работу автоколебательного мультивибратора на биполярных транзисторах.

Как известно, автоколебательный мультивибратор предназначен для формирования периодической последовательности импульсов, форма которых близка к прямоугольной. Мультивибратор на биполярных транзисторах представляет собой двухкаскадное устройство с цепями положительной обратной связи через конденсаторы.

Если номинальные значения компонентов в плечах мультивибратора одинаковы, то схема становится совершенно симметрична и самовозбуждения не происходит. На практике такая ситуация невозможна из-за разброса параметров компонентов схемы. При моделировании симметричных схем, для обеспечения режима самовозбуждения необходимо внести некоторую «искусственную асимметрию». Проще всего это сделать путем задания несимметричных начальных условий.

На рисунке 5.16 показаны принципиальная схема автоколебательного мультивибратора, окно задания параметров анализа и временные диаграммы напряжений на выходах Out1 и Out2 и на базе транзистора Q1 — Vbe(Q1).

Кроме того, на рисунке показано окно режима Performance, в котором задается команда измерения длительности переднего фронта импульсов напряжения на выходе Out1 — Rise_Time = 173,305 мкС. Как видно из рисунка, форма импульсов на выходах мультивибратора далека от прямоугольной именно из-за большой длительности передних фронтов.

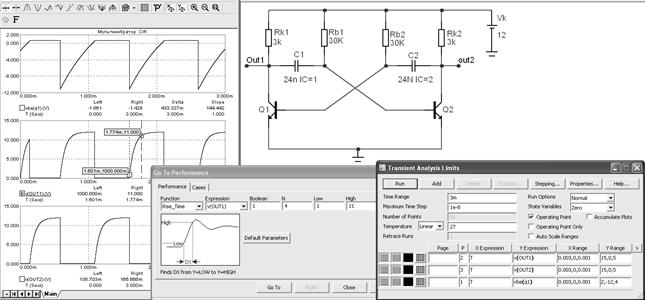
Рисунок 5.16 – Временные диаграммы работы автоколебательного мультивибратора

На практике известны способы улучшения параметров мультивибратора. В частности, необходимо уменьшать величину резистора Rk1. В программе MC9 снижение длительности переднего фронта можно произвести с помощью команды оптимизации, вызываемой нажатием иконки . В появившемся окне (рисунок 5.17) необходимо задать оптимизируемый параметр (в нашем случае - Rk1 ), целевую функцию (Rise_Time) и запустить режим оптимизации.

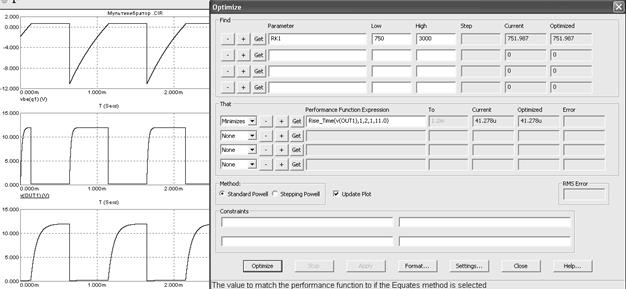
Рисунок 5.17 – Демонстрация режима оптимизации

Видно, что крутизна переднего фронта импульсов на выходе Out1существенно уменьшилась, что видно и в окне оптимизации — 41.278 мкС.

Более подробно режимы PerformanceиOptimiseбудут описаны ниже.

Пример.

Рассмотрим работу амплитудного модулятора на биполярном транзисторе (рисунок 5.18).

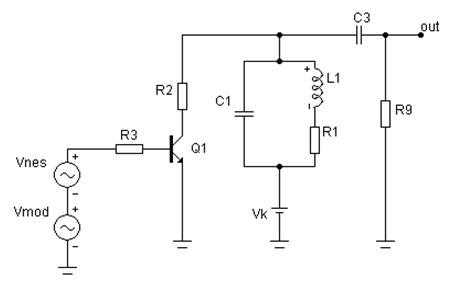
Рисунок 5.18 – Принципиальная схема амплитудного модулятора на биполярном транзисторе

Здесь генератор Vmod вырабатывает гармонический сигнал частотой 25 кГц соответствующий модулирующему сигналу. Генератор Vnes — несущий синусоидальный сигнал с частотой 250 кГц. Колебательный контур L1-C1 настроен на частоту несущей. Смещение на транзисторе выбрано из условия линейности модуляционной характеристики и учтено в постоянной составляющей напряжения генераторов Vmod и Vnes.

Результаты моделирования показаны на рисунке 5.19.

На верхнем графике показаны АМ-колебания, на нижнем — несущая и модулирующий сигнал. На рисунке видно, что уровень несущей и модулирующего сигнала близки, поэтому глубина модуляции близка к 100%. Меняя уровень модулирующего сигнала можно изменять глубину модуляции.

На рисунке 5.20 показаны результаты расчета спектра амплитудномодулированного сигнала. Видно, что в спектре АМ-сигнала присутствуют две боковые составляющие на частотах 225 кГц и 275 кГц, а также составляющая на частоте несущей 250 кГц.

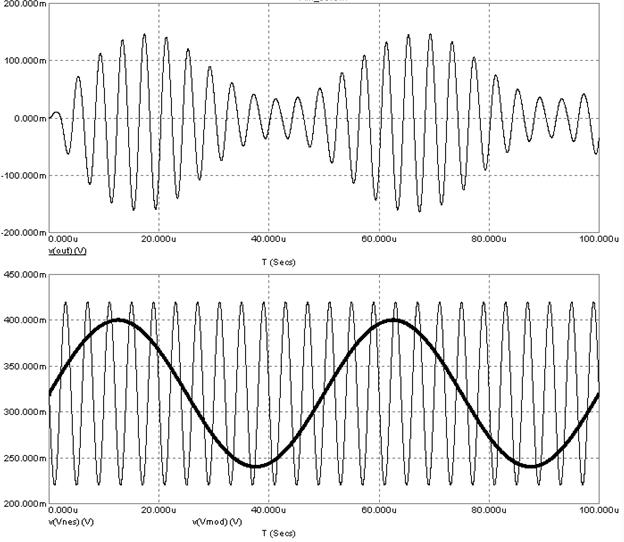
Рисунок 5.19 – Временные диаграммы работы амплитудного модулятора

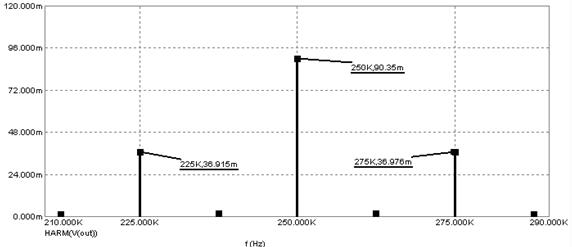
Рисунок 5.20 – Спектр АМ сигнала

Пример.

На практике часто возникает необходимость получить амплитудную модуляцию без несущей, при которой существенно повышаются энергетические показатели передатчиков. Для получения таких сигналов используют балансные модуляторы.

Математическая модель АМ-сигнала без несущей представляет собой произведение модулирующего и несущего колебаний: Vnes * Vmod. Функциональная схема реализации этого математического выражения показана на рисунке 5.21. Здесь же приведены результаты временного анализа балансного модулятора и спектр го сигнала. Анализируя полученные результаты можно сделать выводы:

1. Временная диаграмма АМ-сигнала без несущей имеет характерный перескок фаза в моменты времени, когда модулирующий сигнал меняет знак;

2. В спектре АМ-сигнала без несущей отсутствует составляющая на частоте несущей.Это означает, что не затрачивается энергия на формирование несущей, а следовательно повышаются энергетические показатели.

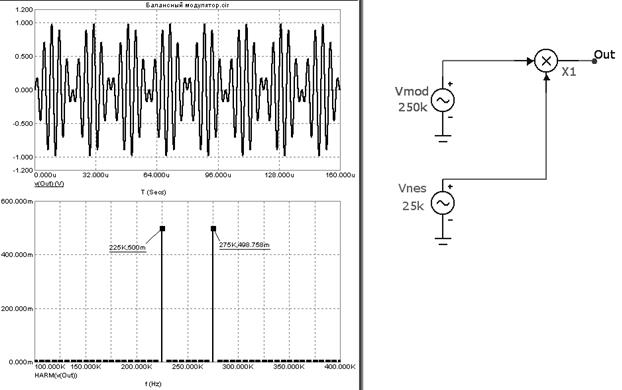
Рисунок 5.21 – Формирование АМ-сигнала без несущей

5.2.8. Анализ частотных характеристик AC

В режиме АС сначала рассчитывается режим схемы по постоянному току, затем линеаризуются все нелинейные компоненты и выполняется расчет комплексных амплитуд узловых потенциалов и токов ветвей. При линеаризации цифровые компоненты заменяются их входными и выходными комплексными сопротивлениями, передача сигналов через них не рассматривается.

Ко входу схемы должен быть подключен источник синусоидального или импульсного сигнала PULSE. Этот источник в режиме AC задает место подключения гармонического возмущения с переменной частотой.

При расчете частотных характеристик комплексная амплитуда этого сигнала по умолчанию автоматически полагается равной 1 В, начальная фаза нулевая, а частота меняется в пределах, задаваемых в меню AC Analysis Limits.

Если имеется один источник сигнала, то выходные напряжения будут совпадать с частотными характеристиками устройства. Если же источников сигнала несколько, то отклики от каждого сигнала будут складываться как комплексные величины.

После перехода в режим анализа частотных характеристик программа МС9 проверяет правильность составления схемы. При отсутствии ошибок в схеме программа открывает окно задания параметров моделирования AC Analysis Limits (рисунок 5.22).

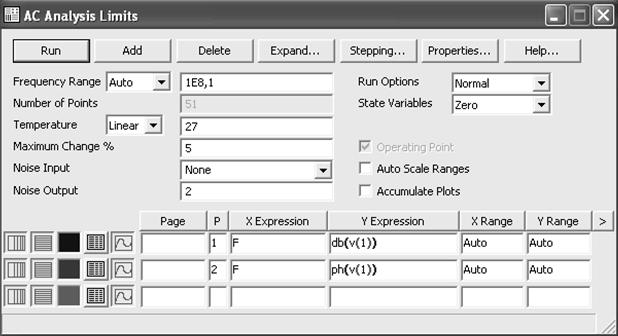
Рисунок 5.22 – Окно задания параметров моделировании в режиме AC.

Как видно из рисунка, набор команд практически не отличается от аналогичных, соответствующих режиму Transient.

Формат задания диапазона частот Frequence Range — fmax[,fmin]. Кроме того, здесь можно выбрать метод вычисления следующей расчетной точки по частоте — Auto, Linear, Log, List.

X Expression — имя переменной, откладываемой по оси X. Обычно при анализе частотных характеристик по этой оси откладывается частота (переменная F), однако это не обязательно. Так при расчете импульсной характеристики с помощью преобразования Фурье по этой оси откладывается время (переменная Т), а при построении годографа для анализа устойчивости по методу Найквиста — действительная составляющая комплексного сигнала.

Y Expression — математическое выражение для переменной, откладываемой по оси Y. Это может быть простая переменная типа напряжения в узле V(5), падение напряжения на двухполюсном компоненте V(L1) или тока ветви I(2,3), I(L1), произведения комплексных величин, например V(VCC)*I(VCC), и другие выражения.

X Range — максимальное и минимальное значение переменной Х на графике по формату High[,Low]. Если минимальное значение Low равно нулю, его можно не указывать. Для автоматического выбора диапазона переменных в этой графе указывается Auto. В этом случае сначала выполняется моделирование, в процессе которого графики строятся в стандартном масштабе и затем автоматически перестраиваются. Удобно также использовать Fmax,Fmin, в этом случае не надо дублировать диапазон, указанный в Frequency Range.

Y Range — максимальное и минимальное значение переменной Y на графике; если минимальное значение равно нулю, его можно не указывать. Для автоматического выбора диапазона переменных в этой графе указывается Auto.

Еще одной особенностью режима AC является возможность вывода графиков как в прамоугольной системе координат , полярной системе координат , а также круговой системе координат т.н. диаграмме Смита.

Последовательность вычислений, выполняемая при проведении анализа частотных характеристик, следующая:

1. Рассчитывается режим работы схемы по постоянному току, исходя из величин постоянных источников напряжения и тока в схеме, а также значений постоянных составляющих источников сигнала схемы (атрибут DC для SINE SOURCE и PULSE SOURСE).

2. Составляется линейная эквивалентная схема замещения каждого прибора на переменном токе в окрестности рассчитанного режима по постоянному току.

3. Составляется полная линеаризованная схема замещения анализируемой схемы по переменному току в окрестности рассчитанного режима по постоянному току (ей соответствует система линейных дифференциальных уравнений).

4. Все источники сигнала схемы принимаются синусоидальными с частотой f = fmin и амплитудой А=1 и нулевой начальной фазой .

5. Анализируется схема и находятся отклики в виде комплексных величин узловых потенциалов и токов схемы для линеаризованной схемы на заданной частоте.

6. Для заданной переменной и для заданных величин (Re, Im, Mag, PHASE и пр.) на графиках строятся точки.

7. Увеличивается частота f на заданный шаг и снова производится расчет. Если частота превысила значение fmax, то расчет завершается.

Пример.

Рассчитаем частотные характеристики однокаскадного резонансного усилителя на биполярном транзисторе. На вход усилителя подается сигнал от генератора V1. В качестве источника питания используется батарея V2. Схема и результаты расчетов показаны на рисунке 5.23.

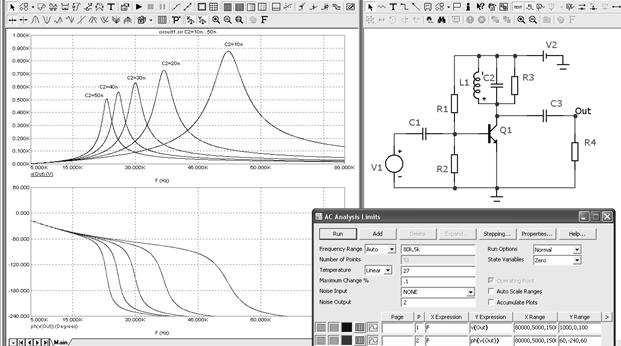
Рисунок 5.23 – АЧХ и ФЧХ резонансного усилителя

Здесь показаны графики проведения многовариантного (пошагового) анализа при изменении номинального значения конденсатора C2. Текстовые надписи соответствующих кривых выполняются по команде Scope > Label Branches .

Пример.

Рассмотрим пример замены некоторого фильтра эквивалентным зависимым источником, задаваемым передаточной функцией.

Пусть задан фильтр в виде следующей принципиальной схемы.

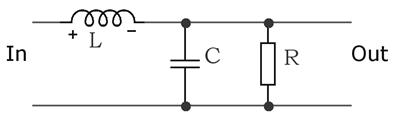
С помощью несложных преобразований можно записать передаточную функцию для заданной схемы в операторной форме:

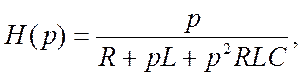
где p — переменная Лапласа.

Теперь создадим в программе МС9 две схемы (рисунок 5.24) — принципиальную схему фильтра, показанную выше, и линейный управляемый источник напряжения заданный передаточной функцией H(p).

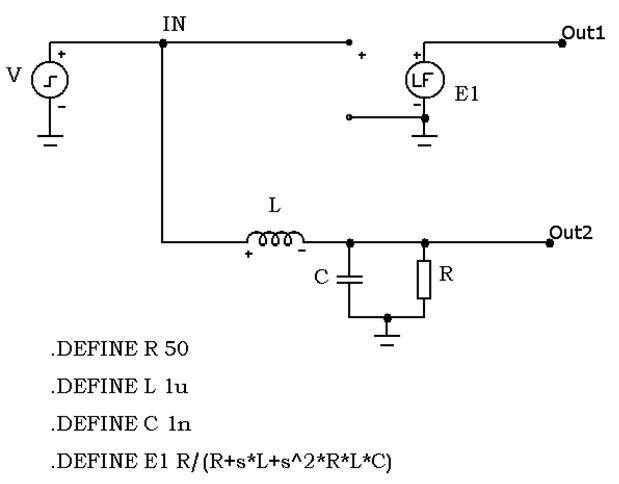
Рисунок 5.24 – Пример замены фильтра управляемым источником

Отметим, что при описании передаточной функции источника напряжения, в качестве переменной Лапласа используется идентификатор s , так как именно он используется для этих целей в европейских странах.

Поведем анализ частотных характеристик представленных устройств — рассчитаем АЧХ для узлов Out1 и Out2. Результаты показаны на рисунке 5.25. Как и следовало ожидать, частотные характеристики совершенно одинаковы. Это дает основания при необходимости заменять принципиальные схемы фильтров их аналогами в виде управляемых источников, что в некоторых случаях существенно облегчает решение задач.

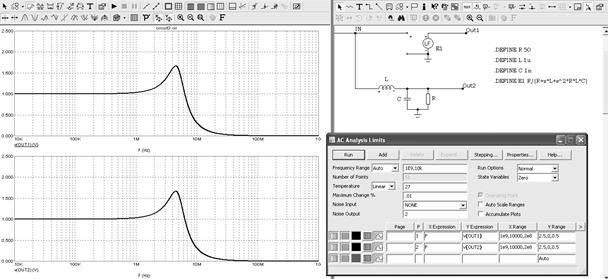
Рисунок 5.25 – Сравнение частотных характеристик

Пример.

Рассмотрим процедуру параметрической оптимизации в режиме анализа частотных характеристик.

Пусть имеется схема, состоящая из трех компонентов – рисунок 5.26. Здесь же приведена АЧХ, рассчитанная для указанных на схеме номинальных значениях компонентов.

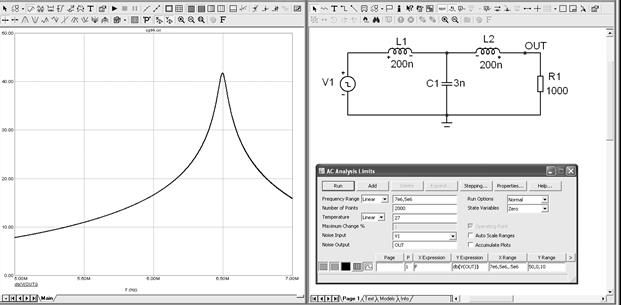
Рисунок 5.26 – Схема и ее АЧХ к примеру 3

Как видно, АЧХ имеет выраженный максимум на частоте 6.5 МГц. Пусть необходимо так подобрать номинальные значения реактивных компонентов, чтобы выполнить три условия:

1) обеспечить значение коэффициента передачи на частоте 6 МГц не меньшим 50дБ;

2) обеспечить значение коэффициента передачи на частоте 5.5 МГц не большим 5дБ;

3) обеспечить значение коэффициента передачи на частоте 6 МГц не большим 3дБ.

Воспользуемся опцией параметрической оптимизации Optimize.Для этого нажатием иконки вызываем окно задания параметров оптимизации (рисунок 5.27), в котором перечисляем оптимизируемые компоненты (L1, L2, C1), задаем их минимальные и максимальные границы, а также записываем условия определения оптимума — желательные значения коэффициента передачи на обозначенных выше частотах. После проведения оптимизации, присваиваем компонентам рассчитанные значения и вновь запускаем расчет АЧХ.

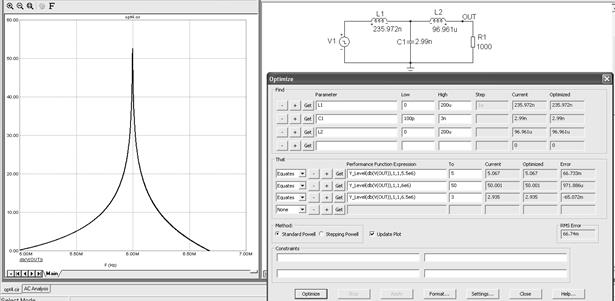
Рисунок 5.27 – АЧХ схемы примера 3 после оптимизации

Как видно из рисунке 5.28 заданные требования к АЧХ выполняются с высокой точностью.