Синтез наблюдателя состояния с зависимыми от времени коэффициентами на основе решения матричной системы сравнения
Пусть снова для рассматриваемой системы требуется синтезировать наблюдатель вида (2.3) вектора состояния x(t) по результатам измерений y(t) (2.1). Матрицу L коэффициентов наблюдателя будем находить из условия минимума следа правой части матричной системы сравнения (2.5). Для этого приравняем нулю производную от следа матрицы правой части МСС (2.5)
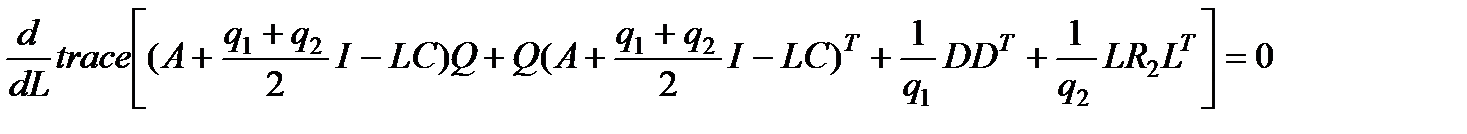 .
.
Отсюда получаем 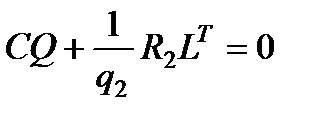 и находим матрицу
и находим матрицу 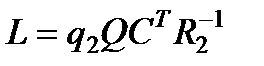 . Вторая производная от следа матрицы правой части по L равна
. Вторая производная от следа матрицы правой части по L равна 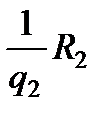 и является положительно определенной матрицей. Поэтому матрица
и является положительно определенной матрицей. Поэтому матрица
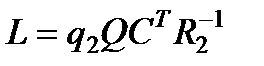 (2.10)
(2.10)
будет доставлять минимум следу матрицы правой части в каждый момент времени t.
Для проверки работоспособности регулятора в виде обратной связи по состоянию наблюдателя с матрицей L коэффициентов из (2.10), определяемых по частному решению матричной системы сравнение (2.5) было выполнено численное моделирование исходной системы с регулятором и наблюдателем. Для этого использовалась функция Observ_CS_NB_Mayat_Integr_02, текст которой представлен ниже. В ней вызывается стандартная функция ode45 для численного интегрирования системы дифференциальных уравнений.
function y= Observ_CS_NB_Mayat_Integr_02(n,x,w0,A,D,K,Cy,R2,R2_1,q1,q2,t0,tk,k)
%Функция для интегрирования нелинейной модели маятника с регулятором
[t,x] = ode45(@(t,x) Prav_CS_Nabl_Mayat_1(t,x,w0,A,D,K,Cy,R2,R2_1,q1,q2),[t0 tk],x);
nh=length(x(:,1));
t(nh)
figure (k)
plot(t,x(:,5),'b');grid on;hold on;
plot(t,x(:,6),'r');grid on;hold on;
plot(t,x(:,7),'y');grid on;hold on;
plot(t,x(:,8),'g');grid on;hold on;
y=[x(nh,1); x(nh,2);x(nh,3);x(nh,4)];
end
Для вычисления правых частей исходной системы дифференциальных уравнений, матричной системы сравнения и уравнений наблюдателя использовалась функция Prav_CS_Nabl_Mayat_1, текст которой представлен ниже.
function dQ=Prav_CS_Nabl_Mayat_1(t,vec_Q,w0,A,D,K,Cy,R2,R2_1,q1,q2)
% Вычисление правой части матричной системы сравнения и определение матрицы
% коэффициентов усиления наблюдателя в текущий момент времени
Q2 = [vec_Q(1) vec_Q(2); vec_Q(3) vec_Q(4)];
L=q2*Q2*Cy'*R2_1;
%ABK=A+B1*K;
ALC=A-L*Cy;
dQQ2= ALC*Q2 + Q2*ALC' +(q1+q2)*Q2+(D*D')/q1+L*R2*L'/q2;
dQQ2=(dQQ2+dQQ2')/2;
%Вычисление правой части исходной нелинейной системы с
% регулятором, заданным матрицей K, по выходу наблюдателя
%и внешними возмущениями, заданными переменной w
x1=[vec_Q(5); vec_Q(6)];
xn=[vec_Q(7); vec_Q(8)];
u=K*xn;
w=-sin(2*cos(3*t));
ksi=(0.5-rand(1))/5000;
y=Cy*x1+ksi;
dx1=x1(2);
dx2=-w0*sin(x1(1))+u+w;
dx3=xn(2)+L(1)*(y-Cy*xn);
dx4=-w0*xn(1)+u+L(2)*(y-Cy*xn);
dx=[dx1;dx2;dx3;dx4];
x3=reshape(dQQ2,4,1);
dQ = [x3;dx];
end
На рисунке 2.4 представлены переходные процессы в исходной системе с регулятором K1 по состоянию наблюдателя с зависимыми от частного решения матричной системы сравнения и определяемыми по соотношению (2.10).
Рисунок 2.4. Переходные процессы в исходной системе (синий и красный) с регулятором по состоянию наблюдателя и наблюдателе (черный и зеленый), с зависимыми от частного решения МСС коэффициентами
