Монотонность и экстремумы функции
Если функция f(x) дифференцируема на интервале 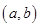 и
и 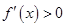
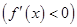
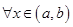 , то
, то 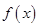 возрастает (соответственно убывает) на этом интервале.
возрастает (соответственно убывает) на этом интервале.
Точка x0 называется точкой локального максимума (локального минимума), если существует такая окрестность U(х0)этой точки, что f(x)< f(х0)" x Î U(х0), x¹x0 (соответственно, f(x) > f(х0)/" x Î
U(х0), x¹x0 ).
Точки локального максимума и минимума называются точками локального экстремума, а значения функции в этих точках — экстремумами функции.
Если 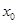 — точка локального экстремума для функции
— точка локального экстремума для функции 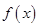 , то в этой точке производная функции либо равна нулю (
, то в этой точке производная функции либо равна нулю ( 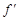 (x0) = 0), либо не существует.
(x0) = 0), либо не существует.
Точки области определения функции 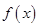 , в которых ее производная не существует или равна нулю, называются критическими точками функции. В силу сформулированной теоремы, экстремумы функции находятся среди ее критических точек.
, в которых ее производная не существует или равна нулю, называются критическими точками функции. В силу сформулированной теоремы, экстремумы функции находятся среди ее критических точек.
Пусть функция f(x) непрерывна в точке 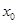 и дифференцируема в некоторой ее окрестности (кроме, быть может, самой точки
и дифференцируема в некоторой ее окрестности (кроме, быть может, самой точки 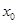 ). Тогда, если (
). Тогда, если ( 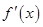 меняет знак при переходе через точку х0, то х0 — точка локального экстремума (если с «+» на «–» — локальный максимум, если же с «–» на «+» — локальный минимум).
меняет знак при переходе через точку х0, то х0 — точка локального экстремума (если с «+» на «–» — локальный максимум, если же с «–» на «+» — локальный минимум).
Если x1, x2,..., xп — критические точки непрерывной на отрезке [а;b] функции 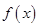 , то наибольшее и наименьшее значения этой функции есть соответственно наибольшее и наименьшее из чисел
, то наибольшее и наименьшее значения этой функции есть соответственно наибольшее и наименьшее из чисел 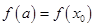 ,
, 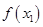 ,
, 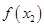 ,...,
,..., 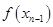 ,
, 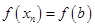 .
.
Выпуклость и вогнутость графика функции.
Точки перегиба
Функция f(x), определенная на интервале 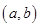 , называется выпуклой вверх (выпуклой вниз) на этом интервале, если точки любой дуги графика функции расположены выше (соответственно, ниже) хорды, стягивающей эту дугу.
, называется выпуклой вверх (выпуклой вниз) на этом интервале, если точки любой дуги графика функции расположены выше (соответственно, ниже) хорды, стягивающей эту дугу.
Иногда выпуклость вверх (соответственно, выпуклость вниз) называют просто выпуклостью (соответственно, вогнутостью).
График выпуклой вверх (выпуклой вниз) на интервале (а; b) функции также называют выпуклым вверх (соответственно, выпуклым вниз).
Можно дать другое, эквивалентное, определение выпуклости вверх (выпуклости вниз): функция f(x) называется выпуклой вверх (выпуклой вниз) на интервале (a; b), если график этой функции при xÎ (а; b) расположен ниже (соответственно, выше) касательной, проведенной в любой его точке (рис. 2.1 а и б).
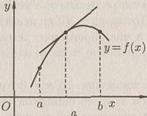
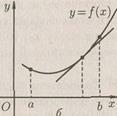
Рис. 2.1
Достаточное условие выпуклости вверх (вниз). Пусть функция f(x) имеет вторую производную на интервале (a;b). Тогда, если 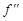 (x ) < 0 (соответственно,
(x ) < 0 (соответственно, 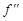 (x )>0) на этом интервале, то функция f(x) выпукла вверх (соответственно, выпукла вниз) на нем.
(x )>0) на этом интервале, то функция f(x) выпукла вверх (соответственно, выпукла вниз) на нем.
Пусть функция f(x) дифференцируема в некоторой окрестности точки x0. Тогда если при переходе через точку x0функция меняет направление выпуклости, то эта точка называется точкой перегиба функции f(x). Точка (x0, f(x0)) при этом называется точкой перегиба графика функции f(x) (рис. 2.2 а и б).
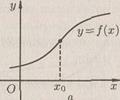
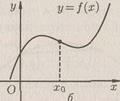
Рис. 2.2
Необходимое условие точки перегиба. Если x0 — точка перегиба функции f(x), то в этой точке вторая производная функция либо равна нулю ( 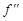 (x0) = 0), либо не существует.
(x0) = 0), либо не существует.
Точки, в которых вторая производная функции равна нулю или не существует, называются критическими точками 2-го рода.
Точки перегиба следует искать среди критических точек 2-го рода.
Достаточное условие точки перегиба. Пусть функция f(x) имеет первую производную в точке x0 и вторую производную в некоторой окрестности этой точки (кроме, быть может, самой точки x0). Тогда если при переходе через точку x0 вторая производная меняет знак, то x0 — точка перегиба.
