Отображение отношения функции

Понятие отображения и функции выражают зависимостью одних переменных величин от других, при этом слово величина может иметь различную смысловую нагрузку. Это может быть элемент любого множества, число, вектор и т.д.

Отображение – множества x во множество y определяется тем, что каждому элементу 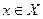ставится в соответствие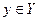

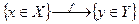- графическое изображение отобра­же­ния, f – обозначение отображения. Закон, который выража­ет­ся или в виде формулы или в виде алгоритма, т.е. последова­тельность действий, которые надо предпринять, чтобы полу­чить зависимость элементов множества y от элементов x. Например: всякая нумерация счетного множества является его отображением на множество натуральных чисел N.

Так как отображение может быть истолковано как соот­ве­тствие, то для того, чтобы показать, что данный элемент x поставлен в соответствие элементу y, пишут 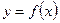и говорят, что y есть образ элемента x при данном отображении f.

Пусть x` - подмножество множества x

y` - подмножество множества y

тогда

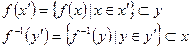
Совокупность элементов множества x, образом которых является y, называется прообразом и обозначается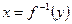

Рассмотрим частные случаи отображения одного множества в другое.

1. Если каждый элемент множества Y имеет прообраз, являя­ющийся элементом множества X,то в этом случае отобра­жение f называется сюръективным.

2. Отображение f называется инъективным, если для каждо­го элемента 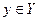существует не более одного прообраза, т.е. при любых 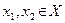, если .

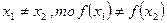Если отображение f сюръективно и инъективно, то оно на­зывается биеткивным или взаимооднозначным.

Рассмотрим на примере три функции, отображающие мно­жество F действительных чисел само на себя:

1) 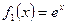- инъективна, но не сюръективна т.к. 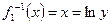, однако не каждый y имеет прообраз x т.к. y>0

2) 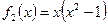- сюръективна, но не инъектина, т.к. y существует при любом x, однако для образа y существует несколько прообразов, т.к. существует несколько корней кубического уравнения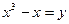

3) 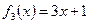- биективна, т.к. x однозначно выражается через x и x однозначно выражается через y.

Два множества называются эквивалентными, если между ними можно установить биективное отображение.

ТОГДА:

Подмножество 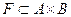называется функцией .

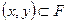Таким образом функцию можно представить в виде графика, причем множество А – область определения функции, а множество В – область значения функции.

Рассмотрим, например, взаимно однозначное отображе­ние множества R на R1, где R1 есть множество всех положи­тельных чисел 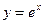. Обратным ему будет отображение 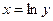. Для таких отображений справедливо следующее тождество:

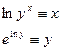
КОМПОЗИЦИЯ

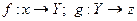, то их композицией (произведением) называют 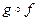, причем, если осуществляется композиция, то 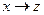. В математике такое отображение называют сложной функцией, y – промежуточный аргумент.

Для композиции справедливо следующие отображения:

- коммутативное -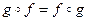

- ассоциативное -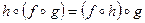

БИНАРНЫЕ ОТНОШЕНИЯ

Квадратом множества А называется декартово произведение множества само на себя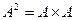

Бинарным отношением Т в множестве А будем называть подмножество его квадрата

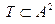
1. Отношение 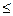выполняется для пар (6,8) (6,6)

2. Отношение имеет общий делитель не равный 1. Выполняется для пар (6,4) (4,2) (8,8) но не выполняется для пар (5,4) (3,8)

3. Любые элементы декартова произведения 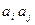находятся в бинарном отношении, если 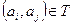, говорят, что 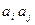связаны отношением Т.

4. Областью значений (изменением бинарного отношения) называется множество 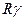, подчиненное условию

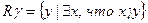
Как известно из курса математики пару (x,y), где 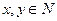изображают на координатной плоскости точкой, тогда множество 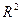отобразится координатной плоскостью, а его подмножество, т.е. бинарное отношение отобразится соответствующими графиками этих отношений.

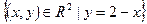
(1)

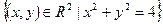
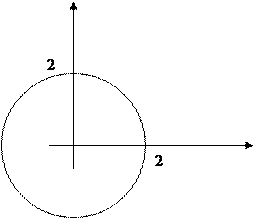(2)

Бинарные отношения на плоскости можно отобразить с помощью графов. Элементы множества 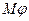обозначаются вершинами графов. Если пара 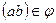, то вершины а и в соединяются звеном.

Например:

(ав)(вс)(ас)(аа)