Коэффициент теплоотдачи

В процессе конвективного переноса тепла характер течения жид­кости имеет очень большое значение, так как им определяется меха­низм теплоотдачи. Процесс переноса тепла на границе с поверхно­стью канала может быть выражен законом Фурье:

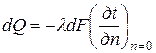, (4.2)

где n – нормаль к поверхности тела.

Это же количество тепла можно выразить уравнением Ньюто­на – Рихмана:

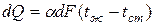. (4.3)

Приравнивая эти уравнения, получаем зависимость:

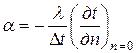. (4.4)

Дифференциальное уравнение (4.4) описывает процесс тепло­обмена на поверхности канала (n = 0).

По своему физическому характеру конвективный теплообмен является весьма сложным процессом и зависит от большого числа факторов, определяющих процесс теплоотдачи. Коэффициент тепло­отдачи характеризует интенсивность теплообмена между жидкостью и поверхностью канала. В общем случае коэффициент теплоотдачи является функцией физических параметров жидкости, характера течения жидкости, скорости движения жидкости, формы и размеров тела и др.

Отсюда коэффициент теплоотдачи можно представить зависимостью:

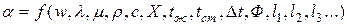, (4.5)

Здесь X – характер движения жидкости (свободная или вынуж­денная конвекция);

Ф – форма стенки;

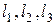– размеры поверхности.

Уравнение (4.5) показывает, что коэффициент теплоотдачи – величина сложная и для ее определения невозможно дать общую формулу. Обычно для определения величины 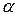приходится прибегать к опыт­ным исследованиям.

Основы теории подобия

Основные понятия

При изучении различных физических явлений применяют два метода исследований, которые позволяют получить количественные закономерности для исследуемых явлений.

В первом методе ис­пользуют экспериментальное изучение конкретных свойств, еди­ничного явления, во втором методе исходят из теоретического исследова­ния рассматриваемой проблемы.

Достоинством экспериментального метода исследования являет­ся достоверность получаемых результатов. Кроме того, при выпол­нении эксперимента основное внимание можно сосредоточить на изучении величин, представляющих наибольший практический интерес.

Основной недостаток экспериментального метода исследования заключается в том, что результаты данного эксперимента не могут быть использованы применительно к другому явлению, которое в деталях отличается от изученного. Поэтому выводы, сделанные на основании анализа результатов данного экспериментального ис­следования, не допускают распространения их на другие явления. Следовательно, при экспериментальном методе исследования каж­дый конкретный случай должен служить самостоятельным объектом изучения. Последнее обстоятельство является органическим недо­статком указанного метода исследований.

Второй метод исследования для нахождения количественных зависимостей, который широко применяется современной наукой, рассматривается в математической или теоретической физике.

При выводе дифференциальных уравнений теоретической фи­зики используются самые общие законы природы, которые в свою очередь являются результатом чрезвычайно широкого обобщения опытных данных. Приложение этих общих законов к изучаемым явлениям позволяет получить наиболее общие связи между физи­ческими параметрами явления.

Таким образом, любое дифференциальное уравнение (или систе­ма уравнений) является математической моделью целого класса яв­лений. Следовательно, под классом понимается такая совокупность явлений, которая характеризуется одинаковым механизмом про­цессов и одинаковой физической природой.

Явления, которые входят в класс, подчиняются одинаковым уравнениям, как по форме записи, так и по физическому содержанию входящих в него величин. Например, дифференциальное уравнение теплопроводности

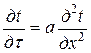
описывает целый класс явлений нестационарной теплопроводности, которые имеют общий механизм процессов.

При интегрировании любого дифференциального уравнения можно получить бесчисленное множество различных решений, удовлетворяющих этому уравнению.

Чтобы получить из множества решений одно частное, надо знать все характерные особенности данного явления, выделяющие его из всего класса однородных явлений. Эти дополнительные условия, которые вместе с дифференциальным уравнением однозначно определяют единичное явление, называют условиями однозначности. Условия однозначности должны содержать все особенности данного конкретного явления.

Условия однозначности характеризуются следующими индиви­дуальными признаками, выделяющими их из целого класса явле­ний. Они состоят:

1) из геометрических условий, характеризующих форму и размеры тела или системы;

2) из физических условий, кото­рыми обладают тела, составляющие данную систему;

3) из граничных условий, которые характеризуют взаимодействие системы с окру­жающей средой (т. е. необходимо знать условия протекания про­цесса на границах тел);

4) из временных условий, характеризующих протекание процесса в начальный момент времени по всему объему системы (для стационарных процессов временные условия от­падают).

Дифференциальные уравнения и четыре условия однозначности определяют конкретное единичное явление. В большинстве случаев и, в частности, в случае описания конвективного теплообмена из-за сложности изучаемых явлений найти решение, удовлетворяю­щее дифференциальным уравнениям и условиям однозначности, невозможно.

Следовательно, если недостатком экспериментального метода исследования является невозможность распространения результа­тов, полученных в данном опыте, на другие явления, отличающиеся от изученного, то недостатком математической физики является не­возможность перейти от класса явлений, характеризуемых диф­ференциальными уравнениями и условиями однозначности, к еди­ничному конкретному явлению. Каждый из этих методов в отдель­ности не может быть эффективно использован для решения практи­ческих задач.

Если положительные стороны математического и эксперимен­тального методов исследования объединить в одно целое, то можно получить универсальный аппарат для изучения различных явлений природы. Такое объединение обоих методов осуществляется тео­рией подобия.

Теория подобия позволяет сделать из дифференциальных урав­нений и условий однозначности ряд выводов, не прибегая к интег­рированию, и тем самым дает теоретическую базу для постановки опытов и обработки экспериментальных данных.