Приток жидкости к группе скважин с удаленным контуром питания

Интерференцией (взаимодействием) называется явление влияния работающих скважин друг на друга. Наиболее наглядно интерференция проявляете в том, что при одинаковых условиях работы скважин суммарный дебит всех скважин растет не прямо пропорционально количеству скважин, а более сложным образом. При этом с увеличением числа скважин пуск каждой новой скважины приводит к меньшему увеличению суммарного дебита, а дебит остальных скважин уменьшается. На рисунке 4.1 для случая кольцевой батареи скважин радиусом сто метров и контуром питания на расстоянии один километр приведены зависимости: 1 – отношение суммарного дебита всех скважин к дебиту одиночной скважины; 2 – асимптотика 1 при n –>∞; 3 – отношение дебита первой скважины к дебиту одиночной скважины.

Рисунок 4.1 – Проявление интерференции скважин: 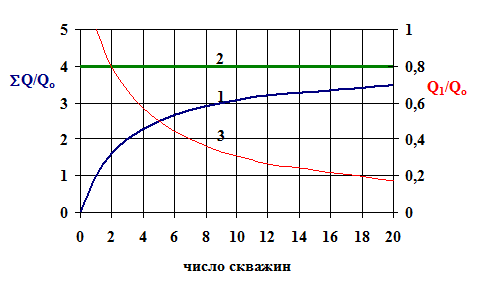1 – отношение суммарного дебита к дебиту одиночной скважины; 2 – асимптотика при n -->∞; 3 – отношение дебита первой скважины к дебиту одиночной скважины

Как видно из графика, при n = 1 отношение суммарного дебита к дебиту одиночной скважины равно единице. При бурении второй, точно такой же скважины, кажется, что суммарный дебит должен увеличится в два раза, но в действительности проявляется интерференция скважин и суммарный дебит увеличивается, не в два раза, а меньше. Это приводит к тому, что, начиная с некоторого, достаточно большого числа скважин, бурить дополнительные добывающие скважины экономически не выгодно. Для того, чтобы обойти это ограничение, необходимо разбить месторождение на отдельные области с поддержанием контурного давления в них. Это обычно достигается бурением нескольких рядов или кольцевых батарей нагнетательных скважин. С бурением каждой новой скважины дебит первой пробуренной скважины уменьшается (линия 3).

Назовем точечным стоком на плоскости точку, поглощающую жидкость. Сток можно рассматривать как гидродинамически совершенную скважину бесконечно малого радиуса в пласте единичной толщины. На плоскости вокруг точечного стока будет радиальное движение.

Точечный источник – это точка, выделяющая жидкость (модель нагнетательной скважины). Различие между источником и стоком – в знаке дебита: у стока дебит положительный Q > 0, а источника – отрицательный Q < 0.

Рассмотрим одиночный точечный сток (добывающую скважину). Распределение давления вокруг скважины выведено в разделе 2.1.2:

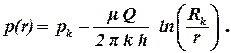(4.1)

Иногда вместо давления вводится понятие потенциала Ф [1], а вместо расхода – удельный расход q. Потенциал и удельный расход определяются следующим образом:

.

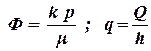(4.2)

Это делается для того, чтобы упростить запись громоздких формул. Например: распределение потенциала (давления) вокруг скважины в этом случае запишется в более простом виде:

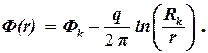(4.3)

Потенциал и удельный расход имеют размерность м²/с.

В подземной гидромеханике при работе группы скважин и установившемся движении несжимаемой жидкости широко используется метод суперпозиции (наложения), который следует из линейности уравнения Лапласа, описывающем распределение давления в пласте (разделе 2.1). Математический смысл метода суперпозиции заключается в том, что если имеется несколько решений уравнения Лапласа p₁(х, у, z), p₂(х, у, z),…, p_n(х, у, z), то и следующая сумма 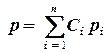также является решением уравнения Лапласа.

Следует при этом подчеркнуть, что подбором произвольных постоянных C_i в суммарном значении давления можно удовлетворить всем граничным условиям.

Гидродинамический смысл метода суперпозиции состоит в том, что изменения давления в любой точке пласта, вызванные работой каждой скважины (добывающей или нагнетательной), алгебраически суммируются в каждой точке пласта. Поэтому будут суммироваться и вектора скоростей фильтрации то, есть принцип суперпозиции применим и векторам скорости фильтрации.

Рассмотрим нефтяное месторождение, которое эксплуатируется n скважинами, с различными дебитами Q_i (рисунок 4.2). Выберем точку М, в которой необходимо найти давление. Обозначим расстояние от оси первой скважины до точки M r_1M, от оси второй скважины до точки M r_2M и так далее. Если первая из этих скважин работает одна, то падение давления в точке M определяется по формуле:

.

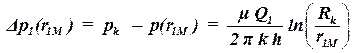(4.4)

Если работает единственная i — тая скважина, то падение давления в точке M будет равно:

.

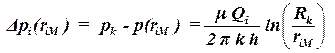(4.5)

По принципу суперпозиции при работе всех скважин падения давления суммируются, поэтому вычисляется по формуле:

.

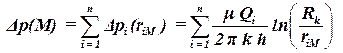(4.6)

По этой формуле можно рассчитать падение давления в любой точке пласта по известным дебитам скважин.

Рисунок 4.2 – 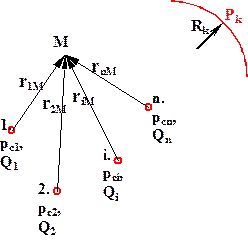Схема группы скважин в пласте с удаленным контуром питания

Но часто встречается задача, когда по известным давлениям на скважинах необходимо рассчитать дебиты скважин.

Для того, чтобы найти n дебитов, необходимо составить систему из n уравнений. Будем обозначать номер уравнения индексом j. Для того, чтобы получить первое уравнение (j = 1) поместим точку M на забой первой скважины, где падение давления известно и равно 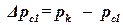. Тогда расстояние от i — той скважины до точки M будет равно r_i1, и первое уравнение запишется:

.

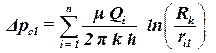(4.7)

Второе уравнение (j = 2) получим, если поместив точку M на забой второй скважины:

,

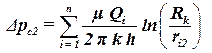(4.8)

а для j — той скважины:

.

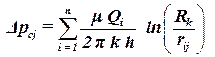(4.9)

Так как индекс j принимает значения от 1 до n, то всю систему уравнений удобно записать в виде:

.

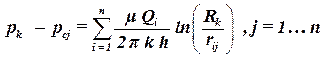(4.10)

Обратите внимание, что расстояния определяются от центра скважины до точки M, поэтому если поместить точку M на забой первой скважины, то расстояние от центра первой скважины до этой точки не равняется нулю, а равно радиусу первой скважины r₁₁ = r_c1. Это относится и к другим скважинам r₂₂ = r_c2; r₃₃ = r_c3 и так далее.

Уточним понятие расстояния до контура питания. Контуром питания может быть любая линия равного давления (изобара), давление на которой обозначается p_k. При работе одиночной скважины в однородном пласте изобарами являются окружности, а расстояние от скважины до контура питания является радиусом этой окружности и обозначается R_k. Если в пласте работают несколько скважин, то изобары не будут являться окружностями и ввести понятия радиуса контура питания нельзя, величина R_k в уравнении (4.10) не определена.

Введем понятие удаленного контура питания. Найдем максимальное расстояние между скважинами, которое обозначим max(r_ij). Выберем изобару на достаточно большом расстоянии от центра скважин. Эта изобара близка к окружности, радиус которой R_k. Если выполняется условие R_k >> max(r_ij), тогда расстояние от любой скважины до любой точки на контуре питания приблизительно равно расстоянию R_k. Контур называется удаленным, если максимальное расстояние между скважинами гораздо меньше расстояния от центра скважин до контура питания. Система уравнений (4.10) справедлива для удаленного контура питания.

Обычно нефтяные месторождения разрабатываются десятками и сотнями скважин, значит надо составить десятки или сотни таких уравнений интерференции скважин. Решение такой сложной системы уравнений возможно с помощью ЭВМ.

Далее рассмотрим использование методов суперпозиции и отображения источников и стоков на некоторых задачах, имеющих практическое применение в теории разработки нефтяных и газовых месторождений.