Выпуклость, вогнутость и точки перегиба функции

Пусть функция f(x) имеет производную в каждой точке промежутка (a;b). Если на промежутке (a;b) график функции f(x) расположен выше любой своей касательной, проведенной в точке этого промежутка, то функция называется вогнутойна этом промежутке (иногда говорят "выпуклой вниз").

Если на промежутке (a;b) график функции f(x) расположен ниже любой своей касательной, проведенной в точке этого промежутка, то функция называется выпуклой на этом промежутке (иногда говорят "выпуклой вверх").

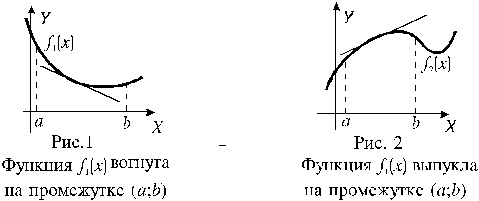
Рис.2.5.4 Рис.2.5.5

Точка x₀ называется точкой перегиба функции f(x), если в этой точке функция имеет производную и существуют два промежутка: (a;x₀) и (x₀;b), на одном из которых функция выпукла, а на другом вогнута.

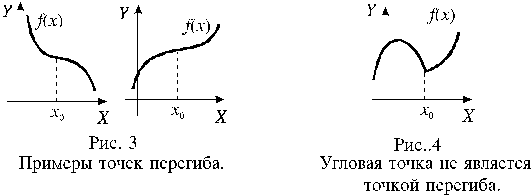
Рис.2.5.6 Рис.2.5.7

Будем называть функцию возрастающей в точке x₀, если она непрерывна в этой точке и возрастает в некоторой ее окрестности. Подобным образом можно определить функцию, убывающую в точке.

Приведем без доказательства важную для исследования функций теорему.

Если f¢¢(x) > 0 на промежутке (a;b), то на этом промежутке функция f(x) вогнута. Если f¢¢(x) < 0 на промежутке (a;b), то на этом промежутке функция f(x) выпукла.

Из положительности второй производной функции на промежутке следует возрастание первой производной на этом промежутке, а это, как показано на рисунке 2.5.8, – признак вогнутой функции. Аналогичным образом иллюстрируется второе утверждение теоремы.

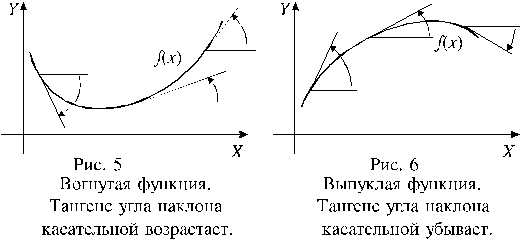
Рис.2.5.8 Рис.2.5.9

Если x₀ – точка перегиба функции f(x), то f¢¢(x₀) = 0.

Приведем другую формулировку достаточных условий экстремума функции.

Если в точкеx₀ выполняются условия:

1) f¢(x₀) = 0; f¢¢(x₀) < 0, тогда x₀ – точка максимума;

2) f¢(x₀) = 0; f¢¢(x₀) > 0, тогда x₀ – точка минимума;

3) f¢(x₀) = 0; f¢¢(x₀) = 0,тогда вопрос о поведении функции в точке остается открытым. Здесь может быть экстремум, например в точке x₀ = 0 у функции y = x⁴, но может его не быть, например в точке x₀ = 0 у функции y = x⁵. В этом случае для решения вопроса о наличии экстремума в стационарной точке можно использовать достаточные условия экстремума, приведенные выше.

Функция полезности

Рассмотрим пример из микроэкономики.

В количественной теории полезности предполагается, что потре­битель может дать количественную оценку (в некоторых единицах измерения) полезности любого количества потребляемого им товара.

Это означает существование функции полезности TU аргумента Q –количества купленного товара. Введём понятие предельной полезности, как добавочной полезности, прибавляемой каждой последней порцией товара. Далее построим двумерную систему координат, откладывая по горизонтальной оси

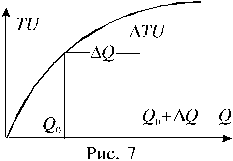количество потребляемого товара Q, а по вертикальной оси – общую полезность TU, как это сделано на рисунке 7. В этой системе координат проведем график функции TU = TU(Q). Точка Q₀ на горизонтальной оси означает количество приобретенного товара, величина DQ –добавочный приобретенный товар. Разность DTU = TU(Q₀ + DQ) – Рис.2.5.10 TU(Q₀) ‑ добавочная полезность, полученная от покупки “довеска” DQ. Тогда добавочная полезность от последней приобретенной порции (или единицы количества) товара вычисляется по формуле DTU / DQ (Курс экономической теории. Под общей редакцией проф. Чепурина М.Н. 1995, стр. 122). Эта дробь, как можно видеть, зависит от величины DQ. Если здесь перейти к пределу при DQ ® 0, то получится формула для определения предельной полезности MU:

.

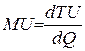Это означает, чтопредельная полезность равна производной функции полезности TU(Q). Закон убывающей предельной полезности сводится к уменьшению этой производной с ростом величины Q. Отсюда следует выпуклость графика функции TU(Q). Понятие функции полезности и представление предельной полезности в виде производной этой функции широко используется в математической экономике.

Раздел 3. Функция нескольких переменных

Тема 3.1. Основные понятия функции нескольких переменных

Пусть имеется n+1 переменная x₁, x₂, ..., x_n, y, которые связаны между собой так, что каждому набору числовых значений переменных x₁, x₂, ..., x_n соответствует единственное значение переменной y. Тогда говорят, что задана функция f от n переменных. Число y, поставленное в соответствие набору x₁, x₂, ..., x_n называется значением функции f в точке (x₁, x₂, ..., x_n), что записывается в виде формулы y = f(x₁,x₂,..., x_n) или y =y(x₁,x₂,..., x_n).

Переменные x₁, x₂, ..., x_n являются аргументами этой функции, а переменная y ‑ функцией от n переменных.

Далее будем говорить лишь о функции двух переменных. Для функций большего числа переменных все факты, о которых будет идти речь, или аналогичны или сохраняются без всякого изменения. Аргументы функции двух переменных будем обозначать как правило x и y, а значение функции - z.

Будем говорить, что заданафункция двух переменных, если любой паре чисел (x,y) из некоторого множества D упорядоченных пар чисел поставлено в соответствие единственное число, которое обозначается f(x,y) и называется значением функции f в точке (x,y).

Множество D называется областью определения функции.

Поскольку любую пару чисел x,y можно рассматривать как пару координат точки M на плоскости, вместо z=f(x,y) можно писать z=f(M).При этом аргументами

функции будут координаты x,y точки M.

Числа x,y можно рассматривать как координаты вектора 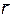, исходящего из начала координат и с концом в точке M(x,y). Тогда функция двух переменных будет функцией вектора, что записывается в виде формулы z = f( 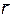), причем аргументами функции являются координаты вектора .

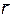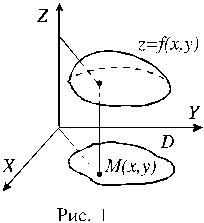
График функции двух переменных есть множество точек (x,y,f(x,y)), где (x,y)ÎD. График представляет собой некоторую поверхность. Пример такой

поверхности приводится на рисунке 1.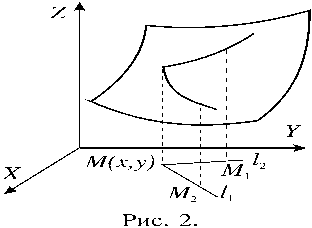

Очевидно, что нельзя ввести понятия возрастания или убывания (монотонности) функции двух переменных. Рассмотрим график некоторой функции z=f(x,y), изображенный на рисун-ке 2. Из точки M(x,y) в плоскости X,Y проведем два луча l₁ и l₂ , определяющих некоторые направления. Можно говорить, что в точке M функция f в направлении l₁ возрастает, а в направлении l₂ убывает. Это означает, что для любой точки M₁ , лежащей на луче l₁ достаточно близко к точке M, выполняется неравенство f(M₁) > f(M). Для любой точки M₂ , лежащей на луче l₂ достаточно близко к точке M, выполняется неравенство f(M₂) < f(M).

Одним из подходов к исследованию функций двух переменных является изучение поведения функции в точке, то есть определение направлений, в которых функция убывает или возрастает, и определение скорости возрастания или убывания.

Можно использовать другой подход. Пусть имеется функция z = f(x,y) c графиком, представляющим собой некоторую поверхность.

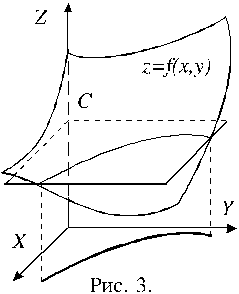Рассмотрим сечение графика функции плоскостью z=C (эта плоскость параллельна плоскости XOY и пересекает ось Z в точке z=C ). Спроектируем линию пересечения этой плоскости с поверхностью z = f(x,y) на плоскость XOY и получим так называемую линию уровня C функции z = f(x,y). Линия уровня представляет собой множество всех точек в плоскости XOY, для которых выполняется равенство f(x,y) = C. Придавая различные значения параметру C, можно получить множество линий уровня функции f(x,y). Если для каждой линии уровня указать соответствующее ей значение C, то получится топографическая карта поверхности, представляющей собой график функции.

В микроэкономике, в предположении что потребитель приобретает лишь два вида товаров: A и B, вводится понятие общей полезности TU, как функции двух аргументов: Q₁ и Q₂ – количеств потребленных товаров A и B, соответственно:

TU = TU(Q₁,Q₂). (3.1.1)

Очевидно, что все линии уровня функции TU(Q₁,Q₂) составляют семейство кривых безразличия(Курс экономической теории. Под общей редакцией проф. Чепурина М.Н. 1995, стр. 125).

Пусть в плоскости XOY заданы две точки: M₀(x₀,y₀) и M₁(x₁,y₁). Расстояние r между этими точками рассчитывается по формуле

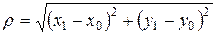. (3.1.2)

Пусть d ‑ некоторое положительное число. d-окрестностью V_d точки M₀(x₀,y₀) называется множество всех точек, координаты x,y которых удовлетворяют неравенствам

.

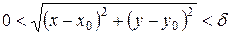Очевидно, что d-окрестность точки M₀(x₀,y₀) представляет собой круг радиуса d с выколотым центром.

Точка M₀(x₀,y₀) называется точкой минимума функции z = f(x,y), если существует такое положительное число d , что из условия M(x,y) Î V_d (x₀,y₀) следует f(x,y) > f(x₀,y₀).

Точка M₀(x₀,y₀) называется точкой максимума функции z = f(x,y), если существует такое положительное число d , что из условия M(x,y) Î V_d (x₀,y₀) следует: f(x,y) < f(x₀,y₀).

Точки минимума и максимума называются точками экстремума.

Число A называется пределом функцииz = f(x,y)в точкеM₀(x₀,y₀):

,

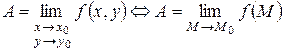если для произвольного числа e > 0 найдется такое число d > 0, что для всех точек M(x,y) из d-окрестности точки M₀(x₀,y₀) выполняется неравенство

|f(x,y) - A|<e .

Функция z = f(x,y)называется непрерывной в точкеM₀(x₀,y₀), если

.

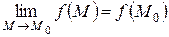Два последних определения фактически повторяют определения предела и непрерывности в точке для функции одной переменной