Прохождение акустической волны через границу жидкость-жидкость

Контролируемая неразрушающими методами среда почти всегда твердая, поэтому случай границы жидкость – жидкость в практике акустического контроля не встречается. Однако на его примере удобно рассматривать основные закономерности отражения и преломления акустических волн, т. к. в жидкостях отсутствуют сдвиги, а следовательно, и поперечные волны (рис. 3.3).

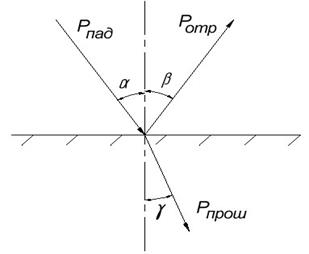Рис. 3.2. Прохождение акустической волны через границу раздела жидкость-жидкость: 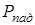, , 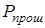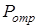– амплитуда падающей, прошедшей и отраженной волн

Запишем выражение для падающей волны в гармоническом виде для плоского случая ( 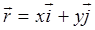) в комплексном виде. Для упрощения пренебрегаем затуханием в среде и опускаем фазовый множитель:

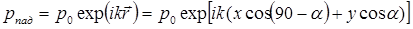, (3.12)

где 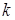– волновой вектор;

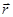– радиус-вектор произвольной точки пространства.

Для отраженной волны

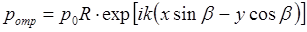. (3.13)

Для прошедшей (преломленной) волны

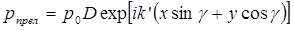, (3.14)

где 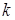и 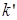– волновые числа соответственно для верхней и нижней среды.

Граничные условия:

1. 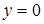– равенство давлений с двух стон от границы радела сред. Тогда можно записать

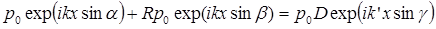. (3.15)

Учтем закон Снеллиуса: 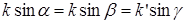. В итоге получаем взаимосвязь между коэффициентами отражения и прохождения по амплитуде:

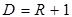. (3.16)

2. 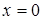– равенство нормальных составляющих колебательных скоростей с двух сторон от границы:

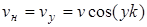, (3.17)

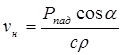, (3.18)

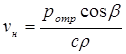, (3.19)

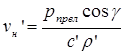, (3.20)

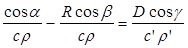. (3.21)

Из выражения (3.21) также можно получить соотношение между коэффициентам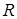и и .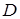

При решении задач о поведении волн на границах сред используют понятие нормального акустического импеданса, который определяют как отношение акустического давления к нормальной составляющей колебательной скорости:

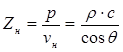, (3.22)

где 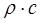– волновое сопротивление среды;

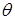– угол между осью 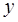и направлением волны.

Нормальные акустические импедансы для падающей, отраженной и прошедшей волны равны соответственно:

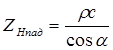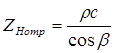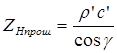, , . (3.23)

Подставив в (3.1) выражения (3.2) для нормальных импедансов, получаем:

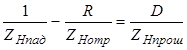. (3.24)

Из граничных условий следует равенство суммарных импедансов сверху и снизу от границы. Суммарным импедансом называют отношение суммы давлений к сумме нормальных составляющих колебательных скоростей для всех волн, существующих по одну сторону от границы:

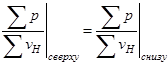(3.25)

или

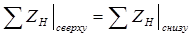. (3.26)

Далее можно показать с учетом (3.23) и (3.25), что

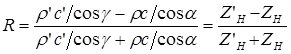, (3.27)

где 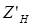– нормальный импеданс снизу от границы;

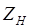– нормальный импеданс сверху от границы.

В общем случае используют суммарные импедансы. Используя равенство давлений, можно доказать, что 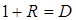. Аналогично можно получить выражение для коэффициента прохождения по амплитуде:

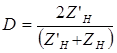. (3.28)

Таким образом, коэффициенты отражения и прохождения зависят от того, из какой среды и в какую переходит волна, т.е. от направления распространения волны.