Волны Лэмба в жидком слое
Нормальная волна Лэмба – комбинация стоячих и бегущих волн. Этот тип волн представляет собой упругие колебания, которые распространяются в волноводах (пластинах и слоях) и имеют фронт, перпендикулярный направлению распространения. Волны Лэмба возникают в жидких и твердых слоях, у которых толщина слоя соизмерима с длиной первичной волны.
Рассмотрим случайнормальных волн в жидком слое (рис. 2.5). На слой жидкости падает под углом α плоская продольная волна. AD – фронт падающей волны; CB – фронт преломленной волны.
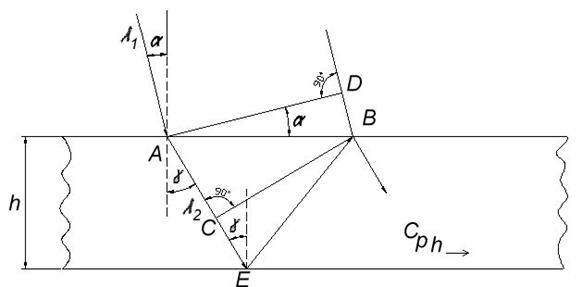 |
Рис. 2.5. Случай нормальных волн в жидком слое: 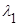 – плоская волна (имеет широкий фронт), – плоская волна (имеет широкий фронт), 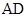 – волновой фронт падающей волны, – волновой фронт падающей волны, 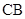 – волновой фронт преломленной волны – волновой фронт преломленной волны |
Преломленная волна многократно отражается от границ пластин. В точке B происходит интерференция падающей и отраженной волн. Условием интерференции является разность хода лучей, кратная l – в этом случае происходит совпадение фаз падающей и отраженной волн.
Таким образом, условие увеличения амплитуды следующее: при определенном угле падения a отраженная от нижней поверхности слоя волна совпадает по фазе с прямой волной, падающей в точке В. Волна распространяется вдоль слоя с фазовой скоростью 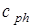 .
.
Путь преломленной волны 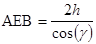 .
.
Запаздывание фазы на пути 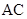 равно
равно 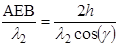 .
.
Запаздывание фазы падающей волны на участке 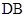 должно быть равно
должно быть равно
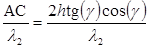 , (2.2)
, (2.2)
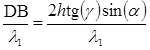 , (2.3)
, (2.3)
где 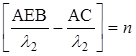 – целое число длин волн. Условие установления резонанса колебаний для случая наклонного падения первичной волны –
– целое число длин волн. Условие установления резонанса колебаний для случая наклонного падения первичной волны –
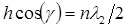 . (2.4)
. (2.4)
При нормальном падении волны 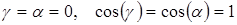 , тогда условие резонанса имеет вид
, тогда условие резонанса имеет вид
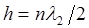 . (2.5)
. (2.5)
Таким образом резонанс колебаний слоя по толщине можно рассматривать как частный случай нормальной волны. В соответствии с законом Снеллиуса:
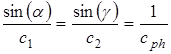 . (2.6)
. (2.6)
Отсюда фазовая скорость нормальной волны Лэмба
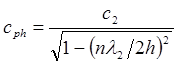 . (2.7)
. (2.7)
Фазовая скорость зависит от следующих факторов:
1) скорости звука в материале пластины;
2) частоты колебаний;
3) толщины слоя.
Моды первого и более высоких порядков ( 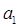 ,
, 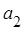 , …,
, …, 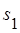 ,
, 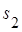 , …) возникают при вполне определенных критических значениях толщин
, …) возникают при вполне определенных критических значениях толщин 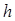 и частот
и частот 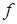 , которые соответствуют резонансным частотам продольных и поперечных объемных волн, причем
, которые соответствуют резонансным частотам продольных и поперечных объемных волн, причем 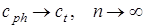 .
.
Напомним, что фазовая и групповая скорости связаны между собой (п. 1.6) через дисперсионное соотношение для скорости:
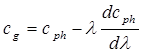 . (2.8)
. (2.8)
При критических значениях 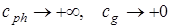 .
.
В научно-технической литературе волны Лэмба часто обозначаются символом SV.
Нормальные волны Лэмба хорошо распространяются в пластинах, трубах, как в волноводе. Данный тип волн чувствителен к неоднородностям волновода, поэтому может применяться для диагностики труб.
Зависимость фазовой скорости лэмбовских волн от частоты отражает отличительную особенность этого вида волн – дисперсию скорости. Графическое описание этого – система дисперсионных кривых (2.1) лэмбовских волн (для разных значений n, рис. 2.6).
 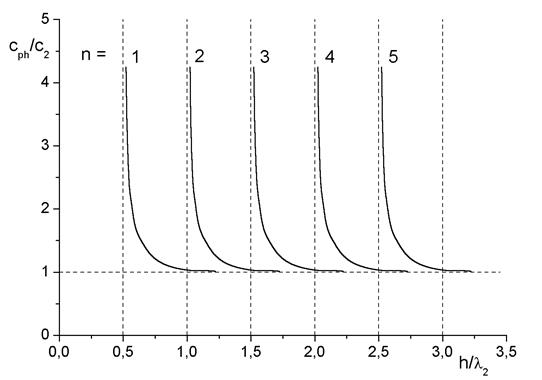 |
Рис. 2.6. Дисперсионные кривые: скорость 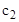 соответствует скорости продольной волны, соответствует скорости продольной волны, 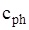 – фазовая скорость лэмбовской волны, h – толщина слоя, – фазовая скорость лэмбовской волны, h – толщина слоя, 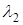 – длина волны, n – порядок дисперсионной кривой – длина волны, n – порядок дисперсионной кривой |
Особенности дисперсионной зависимости:
1. В тех точках, где 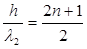 ,
, 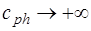 . Физически это означает, что вся поверхность колеблется одновременно, то есть возникает резонанс по толщине.
. Физически это означает, что вся поверхность колеблется одновременно, то есть возникает резонанс по толщине.
2. При 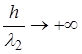
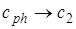 . Данное явление существенно для пластин большой толщины и при работе на высокой частоте.
. Данное явление существенно для пластин большой толщины и при работе на высокой частоте.
Лэмбовские волны с нечетным 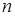 называют симметричными модами (обзначение si), волны с четным
называют симметричными модами (обзначение si), волны с четным 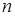 – антисимметричными (ai) . Эти названия отражают характер движения частиц при распространении волн Лэмба.
– антисимметричными (ai) . Эти названия отражают характер движения частиц при распространении волн Лэмба.
