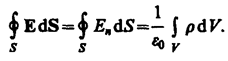Поток вектора напряжённости. Теорема Гаусса для электростатического поля в вакууме
Основные характеристики электростатического поля. Напряжённость и потенциал.
Электрическое поле характеризуется воздействием на электро заряженную частицу с силой пропорциональной заряда частицы и независящей от ее скорости.
Напряжённость
Напряжённость — векторная величина определяющая силу действующую на заряженную частицу или тело со стороныэлектрического поля и численно равная отношению силы к заряду частицы.
Е = F/Q [Н/Кл] или [B/M]
Напряжённость — это основная характеристика электрического поля которая измеряет интенсивность поля.
Направление вектора напряжённости совпадает с направлением силы действующей на частицу с положительным зарядом.
Электрическое поле называется однородным (равномерным) если напряжённость поля во всех точках одинаковое по величине и направлению.
Электрическое напряжение
Электрическое напряжение (U) — это работа (А) совершаемая силой поля по перемещению заряженных частиц между двумя точками поля.
U = A/q [Дж/Кл] или [В]
Потенциал
Потенциал (φ) — это энергетическая характеристика поля численно равная отношению потенциальной энергии заряженной частицы помещенной в данной точке поля величине её заряда.
φ = W/Q[В]
Геометрическое место поля с с одинаковым потенциалом называетсяэквипотенциальной поверхностью.
Поток вектора напряжённости. Теорема Гаусса для электростатического поля в вакууме.
Введем новую физическую величину, характеризующую электрическое поле – поток вектора напряженности электрического поля(Φ). Понятие потока вектора 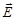 аналогично понятию потока вектора скорости при течении несжимаемой жидкости. Фактически поток вектора
аналогично понятию потока вектора скорости при течении несжимаемой жидкости. Фактически поток вектора 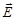 пропорционален числу линий напряженности, пронизывающих элементарную площадку ΔS.
пропорционален числу линий напряженности, пронизывающих элементарную площадку ΔS.
Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка ΔS. Произведение модуля вектора 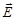 на площадь ΔS и на косинус угла α между вектором
на площадь ΔS и на косинус угла α между вектором 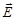 и нормалью
и нормалью 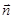 к площадке называется элементарным потоком вектора напряженности через площадку ΔS:
к площадке называется элементарным потоком вектора напряженности через площадку ΔS:
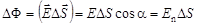 ,
,
где 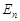 – проекция вектора
– проекция вектора 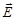 на нормаль
на нормаль 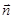 к площадке
к площадке 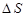 ;
; 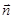 ‑ единичный вектор, перпендикулярный площадке
‑ единичный вектор, перпендикулярный площадке 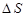 .
.
Полный поток вектора напряженности 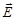 сквозь поверхность
сквозь поверхность 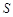 в общем случае равен:
в общем случае равен:
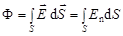 ,
,
где 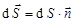 . (Выбор нормали
. (Выбор нормали 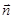 условен, но в случае замкнутых поверхностей
условен, но в случае замкнутых поверхностей 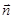 принято брать наружу области, охватываемой этими поверхностями, т. е. выбирать внешнюю нормаль). Единица измерения потока ‑ В·м.
принято брать наружу области, охватываемой этими поверхностями, т. е. выбирать внешнюю нормаль). Единица измерения потока ‑ В·м.
Рассмотрим теперь некоторую произвольную замкнутую поверхность S. Если разбить эту поверхность на малые площадки ΔSi, определить элементарные потоки 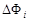 поля
поля 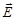 через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора
через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора 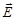 через замкнутую поверхность S
через замкнутую поверхность S
Немецким ученым К. Гауссом (1777—1855) была доказана теорема, определяющая поток вектора напряженности электрического поля сквозь произвольную замкнутую поверхность.
В соответствии с выводами предыдущего раздела, поток вектора напряженности сквозь сферическую поверхность радиусаr, охватывающую точечный заряд Q, находящийся в ее центре, будет равен
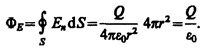
Этот результат справедлив для замкнутой поверхности любой формы.
Действительно, если окружить сферу произвольной замкнутой поверхностью, то каждая линия напряженности, пронизывающая сферу, пройдет и сквозь эту поверхность.
Если замкнутая поверхность произвольной формы охватывает заряд (рисунок слева), то при пересечении любой выбранной линии напряженности с поверхностью она то входит в нее, то выходит из нее.
Если замкнутая поверхность не охватывает заряда, то поток сквозь нее равен нулю, так как число линий напряженности, входящих в поверхность, равно числу линий напряженности, выходящих из нее.
Таким образом, для поверхности любой формы, если она замкнута и заключает в себя точечный заряд Q, поток вектора Е будет равен Q/e0, т. е. теорема Гаусса не теряет справедливости.
Рассмотрим общий случай произвольной поверхности, окружающей nзарядов.
Вводя суммирование под знак интеграла, записываем, что
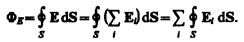
Согласно закону Гаусса, каждый из интегралов, стоящий под знаком суммы, равен Qi/e0.Следовательно,
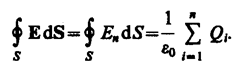
Полученная формула выражает теорему Гаусса для электростатического поля в вакууме:
поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на e0.
В общем случае электрические заряды могут быть размещены с некоторой объемной плотностью r=dQ/dV.. Тогда суммарный заряд, заключенный внутри замкнутой поверхности S, охватывающей некоторый объем V,
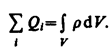
Используя эту формулу, теорему Гаусса можно записать так