Решение квадратичных сравнений по простому модулю
Пусть дано сравнение x2≡a(mod p), p>2 – простое и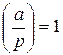 
.
Данное сравнение имеет 2 решения. Укажем, как найти эти решения.
Для p возможны следующие случаи:
p:
p≡3(mod 4) p≡1(mod 4)
 |  |
p≡5(mod 8) p≡1(mod 8)
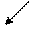p≡9(mod 16) p≡1(mod 16)
И т. д.
а)Пусть p≡3(mod 4), т.е. p=4k+3.
По критерию Эйлера,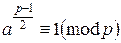 
. Подставляя сюда p, получим
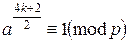
a2k+1≡1(mod p)
a2k+2≡a(mod p)
Вернувшись сравнению, которое требуется решить, заметим, что x2≡a2k+2(mod p), и тогда x≡±ak+1(mod p) – искомое решение.
б) p≡5(mod 8), т.е. p=8k+5.
Найдем какой-нибудь квадратичный невычет по модулю p. Согласно св-ву 7 для символа Лежандра, таким невычетом в случае p=8k+5 будет являться «2». Тогда, согласо критерию Эйлера, 24k+2≡—1(mod p).
Так как a – квадратичный вычет по модулю p, то по критерию Эйлера,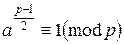 
.
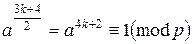Тогда возможны два варианта: a2k+1≡1(mod p) или a2k+1≡—1(mod p).
В первом случае дальнейшие рассуждения проводим как в пункте а, и получаем x≡±ak+1(mod p).
Рассмотрим подробнее второй случай. Имеем:
a2k+1≡—1(mod p)
Для того, чтобы избавиться от знака (—) в правой части, домножим левую часть этого сравнения на 24k+2, а левую – на –1.
24k+2a2k+1≡1(mod p)
24k+2a2k+2≡a(mod p)
x≡±22k+1ak+1(mod p)
Таким образом, имеются два кандидата на решение:
x≡±ak+1(mod p).
x≡±22k+1ak+1(mod p)
Вычислив и подставив каждое из них в исходное сравнение, выберем ту пару, которая удовлетворяет исходному сравнению.
в) p≡9(mod 16), т.е. p=16k+9.
Найдем N – какой-нибудь квадратичный невычет по модулю p. Тогда по критерию Эйлера,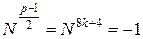 
.
С другой стороны, поскольку a – квадратичный вычет по модулю p, то по критерию Эйлера,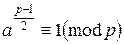 
.
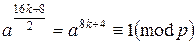Тогда возникают два случая: a4k+2≡1(mod p) или a4k+2≡-1(mod p).
Рассмотрим первый случай: a4k+2≡1(mod p). Поскольку показатель степени в левой части сравнения – четный, то вновь возникают два варианта: a2k+1≡1(mod p) или a2k+1≡—1(mod p), первый из которых приводит, как ранее, к кандидату в решение x≡±ak+1(mod p), а второй вариант, рассуждая как в пункте б, приведем к кандидату в решения x≡±N4k+2ak+1(mod p).
Рассмотрим второй случай: a4k+2≡-1(mod p). Для того, чтобы избавиться от знака (—) в правой части сравнения, домножим правую часть на N8k+4, а левую – на –1. Получим N8k+4a4k+2≡1(mod p). Поскольку показатели степеней в левой части получившегося сравнения четны, то отсюда возникают два варианта: N4k+2a2k+1≡1(mod p) или N4k+2a2k+1≡-1(mod p).
Рассмотрим первый из вариантов:
N4k+2a2k+1≡1(mod p)
N4k+2a2k+2≡a(mod p)
x≡±N2k+1ak+1(mod p).
Рассмотрим второй из вариантов:
N4k+2a2k+1≡-1(mod p)
N12k+6a2k+1≡1(mod p)
N12k+6a2k+2≡a(mod p)
x≡±N6k+3ak+1(mod p)
Итак, получили четыре пары – кандидата на решение:
x≡±ak+1(mod p)
x≡±N2k+1ak+1(mod p)
x≡±N4k+2ak+1(mod p)
x≡±N6k+3ak+1(mod p)
Вычислив и подставив в исходное сравнение, выберем ту пару, которая удовлетворяет исходному сравнению.
Рассмотренным способом можно построить решение для любого простого модуля p. Если p=2hk+2h—1+1, то при решении сравнения возникнет 2h—2 пар – кандидатов в решение, каждая из которых будет иметь вид x≡±Nz(2k+1)ak+1(mod p), где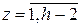 
.
Главная проблема здесь – отыскание квадратичного невычета N, но поскольку, как было доказано ранее, квадратичных вычетов и невычетов по простому модулю – одинаковое количество, то невычет обязательно найдется.
Пример:
Решить сравнение x2≡8(mod 17).
17 – простое число. Выясним, имеет ли данное сравнение решение:
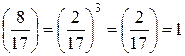. Сравнение имеет 2 решения. Отыщем их.
17=2·8+1=4·4+1=8·2+1=16·1+1=32·0+17=25·0+17.
h=5, k=0. Имеется 23=8 пар-кандидатов в решения.
Найдем какой-нибудь невычет по модулю 17:
.
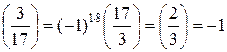Итак, N=3 – кв. невычет по модулю 17.
Имеются следующие кандидаты в решения сравнения:
1) x≡±8(mod 17) 5) x≡±348(mod p)
2) x≡±3·8(mod 17) 6) x≡±358(mod p)
3) x≡±328(mod 17) 7) x≡±368(mod p)
4) x≡±338(mod 17) 8) x≡±378(mod p)
Будем проверять каждую пару решений, пока не найдем верное решение.
1) x≡±8(mod 17). Тогда x2≡64≡13(mod 17).
2) x≡±3·8≡±24≡±7(mod 17). Тогда x2≡49≡15(mod 17).
3) x≡±328≡±72≡±4(mod 17). Тогда x2≡16(mod 17).
4) x≡±338≡±216≡±12(mod 17). Тогда x2≡144≡8(mod 17).
Ответ: x≡±12(mod 17), или x≡±5(mod 17).