Нахождение первообразных корней по простому модулю
В настоящем пункте будем рассматривать число n, причем n—1= 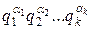 * - каноническое разложение на простые сомножители.
* - каноническое разложение на простые сомножители.
Теорема
On(a)=n—1 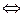 1) an—1≡1(mod n);
1) an—1≡1(mod n);
2) 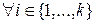 ,
, 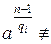 1(mod n).
1(mod n).
Доказательство:
Пусть On(a)=n—1. Тогда (1) выполняется в силу определения порядка элемента в группе. Кроме того, 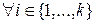 , 1 ≤
, 1 ≤ 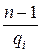 < n—1= On(a), откуда в силу определения порядка элемента, выполняется (2).
< n—1= On(a), откуда в силу определения порядка элемента, выполняется (2).
Пусть теперь выполнены (1) и (2). Покажем, что On(a)=n—1.
В силу (1), On(a)\(n—1). В силу (2), On(a) не делит 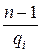
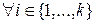 . Значит, On(a)=n—1.
. Значит, On(a)=n—1.
□
Результатами только что доказанной теоремы можно пользоваться для нахождения порождающего элемента группы Up, причем проверять стоит только второй пункт, так как первый для простого модуля выполняется автоматически согласно теореме Ферма. Кроме того, можно вывести правило: если a1, a2 не являются порождающими элементами группы Up, то a1a2 также не является порождающим элементом Up. Отсюда делаем вывод о том, что наименьший порождающий элемент группы Up – простое число.
Пример
p=71. p—1=70=2·5·7.
Для того чтобы a являлся порождающим элементом, необходимо и достаточно, чтобы выполнялись условия: a10 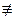 1(mod n), a14
1(mod n), a14 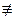 1(mod n), a35
1(mod n), a35 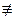 1(mod n).
1(mod n).
Будем испытывать числа из U71. Вместо ab mod 71 для краткости будем писать ab.
2: 210 =30, 214 =54, 235=1. 2 не является порождающим элементом.
3: 310 =48, 314 =54, 335=1. 3 не является порождающим элементом.
5: 510 = 1. 5 не является порождающим элементом.
7: 710 =45, 714 =54, 735=70. 7 – порождающий элемент.
Итак, наименьший порождающий элемент группы U71 (или первообразный корень по модулю 71) есть 7.
Существование и количество первообразных корней.
Первообразные корни существуют не для всякого модуля. Действительно, как было показано в Примере 2 п.1, не существует первообразных корней по модулю 8.
Теорема 1
Первообразные корни по модулю m существуют 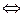 m=2, 4, pα или 2pα, где p – простое нечетное число.
m=2, 4, pα или 2pα, где p – простое нечетное число.
Теорема 2
Количество первообразных корней по модулю m, если они существуют, есть φ(φ(m)).
Пример:
Определить количество первообразных корней по модулю 10.
10 = 2·5=2р. Первообразные корни существуют. Найдем их количество.
φ(φ(10))=φ(4)=2.
Проверим результат. U10={1, 3, 7, 9}
O10(1)=1;
32=9, 33=7, 34=1. O10(3)=4=φ(10). 3 – первообразный корень.
72=9, 73=3, 74=1. O10(7)=4=φ(10). 7 – первообразный корень.
92=1. O10(9)=2.
Действительно, нашлись два первообразных корня по модулю 10.
Теорема 3
Пусть с=φ(m), q1, q2, … , qk – различные простые делители с. Тогда g: (g,m)=1 – первообразный корень по модулю m 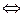 не выполняется ни одно из сравнений
не выполняется ни одно из сравнений 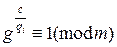 , i=1,2,…,k.
, i=1,2,…,k.
■
Теорема, доказанная в предыдущем пункте, является частным случаем данной теоремы при простом n.
Дискретные логарифмы.
Если g – первообразный корень по модулю m (порождающий элемент Um), то, если γ пробегает полную систему вычетов по модулю φ(m), то gγ пробегает приведенную систему вычетов по модулю m.
Для чисел a: (a,m)=1 введем понятие об индексе, или о дискретном логарифме.
Если a≡gγ (mod m), то γ называется индексом, или дискретным логарифмом числа а по основанию g по модулю m.
В теории чисел принято употреблять слово «индекс» и писать γ=indga, но в криптографии применяют сочетание «дискретный логарифм» и пишут γ=logga. Поскольку на протяжении настоящего пособия не раз встретится упоминание о так называемой задаче дискретного логарифмирования, будем употреблять последний вариант названия и написания. Тем более, что дискретные логарифмы обладают некоторыми свойствами логарифмов непрерывных:
Свойство 1: Дискретный логарифм разнозначен в полной системе вычетов по модулю φ(m).
Свойство 2: loggab…h≡logga+loggb+…+loggh (mod φ(m)).
Свойство 3: loggan≡nlogga(mod φ(m)).
Доказательство этих свойств не представляет сложности и является прямым следствием определений дискретного логарифма и первообразного корня.
