Теоретические сведения, рекомендации и пояснения к выполнению домашних заданий

Московский государственный технический университет им. Н.Э. Баумана

УТВЕРЖДАЮ

Заведующий кафедрой ИУ-6 «Компьютерные системы и сети»

_____________ А.В. Пролетарский

СХЕМОТЕХНИКА ЭВМ

Методические указания к домашним заданиям

«Синтез и анализ комбинационных схем».

Москва 2015

Данные методические указания составлены в соответствии с учебным планом «Направление подготовки-230100-Информатика и вычислительная техника, Профиль-Вычислительные машины, комплексы, системы и сети, Квалификация-бакалавр» и программой дисциплины «Схемотехника ЭВМ», рассмотрены и одобрены кафедрой ИУ6 «Компьютерные системы и сети».

Московский государственный технический университет им. Н.Э. Баумана

Автор В.Ф. Жирков

Введение

Учебным планом по дисциплине «Схемотехника ЭВМ» предусмотрены три домашних задания в пятом семестре.

Цель домашних заданий – синтез и анализ комбинационных схем.

Теоретический подход к синтезу комбинационных схем широко освещается в технической литературе. Однако при практическом применении комбинационных схем, к которым относятся типовые функциональные узлы ЭВМ и цифровых устройств (дешифраторы, шифраторы, мультиплексоры, демультиплексоры, сумматоры, узлы контроля, преобразователи кодов и др.) и специализированные узлы, при анализе их функционирования разработчик сталкивается с явлением возникновения ложных выходных сигналов, не предусмотренных теоретической моделью схемы на языке алгебры логики. Ложные выходные сигналы возникают потому, что теоретическое описание работы схемы не учитывает переходные процессы в источниках входных сигналов, задержки входных сигналов схем, поступающих от разных источников, по линиям связи различной длины, претерпевающих временные задержки и искажения фронтов и спадов сигналов. В этих случаях говорят о гонках, или состязаниях, входных (двух и более) сигналов, приводящих к этому нежелательному явлению. Учет этих факторов затруднен, а в большинстве практических случаев невозможен. Наиболее эффективным способом исключения ложных выходных сигналов, вызванных гонками входных сигналов, является стробирование в асинхронных комбинационных схемах и синхронизация приема выходных сигналов комбинационных схем на входах синхронных триггеров.

Вопросам теоретического синтеза комбинационных схем, анализу их работы, выявлению и объяснению появления ложных выходных сигналов и их устранению с помощью стробирования и синхронизации приема сигналов в запоминающие элементы (триггеры) посвящены три домашних задания, объединенных общей темой «Синтез и анализ комбинационных схем».

Задачами, которые решаются в процессе выполнения домашних заданий, являются:

-освоение методики синтеза комбинационных схем;

-выполнение анализа функционирования комбинационных схем;

-выявление помех в комбинационных схемах, не предусмотренных математическим описанием (моделью) схем функциями алгебры логики и вызванных гонками (состязаниями) входных сигналов и переходными процессами в схемах;

-освоение эффективного метода борьбы с помехами, вызывающими риски сбоя в комбинационных и последовательностных схемах;

-введение стробирования и синхронизации (тактирования).

В данных методических указаниях предлагаются домашние задания №1, №2 и №3 «Синтез и анализ комбинационных схем», которые выполняются последовательно.

Домашние задания

«Синтез и анализ комбинационных схем»

Дана:функция алгебры логики (ФАЛ) f(x₄, x₃, x₂, x₁) четырех переменных x₄, x₃, x₂, x₁. ФАЛ определена номерами наборов, на которых она равна единице.

Требуется выполнить:

1.1 Домашнее задание №1:

-составить таблицу истинности ФАЛ;

-по таблице истинности найти совершенные дизъюнктивную и конъюнктивную нормальные формы ( СДНФ и СКНФ ) функции f(x₄, x₃, x₂, x₁); представить СДНФ и СКНФ функции на картах Карно;

-минимизировать функцию f(x₄, x₃, x₂, x₁), определив ее минимальные дизъюнктивную и конъюнктивную нормальные формы (ДНФ и КНФ);

-преобразовать минимальные ДНФ и КНФ ФАЛ f(x₄, x₃, x₂, x₁) в базисы функций И-НЕ и ИЛИ-НЕ соответственно;

-составить логические схемы в базисах логических элементов (ЛЭ) И-НЕ и ИЛИ-НЕ, реализующих заданную ФАЛ;

-провести анализ временных диаграмм работы логических схем в базисах ЛЭ И-НЕ и ИЛИ-НЕ, выявить ложные сигналы на выходе, вызванные гонками входных сигналов.

1.2 Домашнее задание №2:

-преобразовать минимальные ДНФ и КНФ ФАЛ f(x₄, x₃, x₂, x₁), введя в функции сигнал стробирования, составить логические схемы в базисах ЛЭ И-НЕ и ИЛИ-НЕ и устранить ложные сигналы на выходе логических схем с помощью сигнала стробирования;

-определить временное положение сигнала стробирования.

1.3 Домашнее задание №3:

-устранить ложные сигналы логических схем в базисах ЛЭ И-НЕ и ИЛИ-НЕ, реализующих заданную ФАЛ, с помощью синхронизации приема выходных сигналов комбинационных схем в синхронные триггеры.

Варианты функций алгебры логики домашних заданий, 1-я гр.

«Синтез и анализ комбинационных схем»

№ варианта	Номера наборов переменных, на которых функция алгебры логики равна единице	Фамилия, имя, отчество студента	Подпись	Дата выдачи задания
	1,2,3,4,7,8, 12,13,15
	0,2,3,4, 6,11,13,15
	0,4,7,8,9,11,12,15
	1,2,3,6,10,13,14,15
	1,4,7,9,10,11,12,15
	1,4,7,8,10,12.13,14,15
	2,4,5,6,8,11,14,15
	0,1,2,3,7,8,9.12,14,15
	1,4,5,6,7.10,11,13
	3,4,7,10,11,13,14,15
	0,3,4,5,6,9,11,12,14
	0,3,7,8,10,11,12,14,15
	1,2,3,5,6,7,9,11,12
	0,2,4,6,8,11,12,14
	1,2,4,6,7,8,10,14
	1,3,4,5,7,10,11,12,14
	0,4,5,6,7,8,9,11,12,15
	2,5,6.7,9,11,12,14
	3,5,6,8,11,13,14,15
	0,1,3,7,9,10,11,13
	3,5,7,10,11,12,14,15

Варианты функций алгебры логики домашних заданий, 2-я гр.

«Синтез и анализ комбинационных схем»

№ варианта	Номера наборов переменных, на которых функция алгебры логики равна единице	Фамилия, имя, отчество студента	Подпись	Дата
1	1,3,7,8,9,12,14,15
	0,3,5,7,8,10,11,12
	0,1,3,4,8,11,12,14,15
	0,3,4,7,8,11,14,15
	0,1,3,4,5,9,10,13,14
	0,2,3,4,7,8,12,13,15
	0,2,3,4,6,11,13,15
	0,4,7,8,9,11,12,15
	1,2,3,6,10,13,14,15
	1,4,7,9,10,11,12,15
	1,4,7,8,10,12,13,14,15
	2,4,5,6,8,12,14,15
	0,1,2,3,7,8,9,10,14,15
	1,4,5,6,7,10,11,13
	3,4,7,10,11,13,14,15
	0,3,4,5,6,9,11,12,14
	0,3,7,8,10,11,12,14,15
	1,2,3,5,6,7,9,11,12
	0,2,4,6,8,11,13,15
	1,2,4,6,7,8,10,14
	1,3,4,5,7,10,11,12,14

Варианты функций алгебры логики домашних заданий, 3-я гр.

«Синтез и анализ комбинационных схем»

№ варианта	Номера наборов переменных, на которых функция алгебры логики равна единице	Фамилия, имя, отчество студента	Подпись	Дата выдачи задания
1	0,3,4,6,7,9,10,11,12
	0,1,6,7,8,9,11,15
	0,3,4,7,8,12,14,15
	2,5,6,7,9,10,11,13
	0,3,4,7,10,13,14,15
	0,3,4,5,6,7,10,12,13
	0,1,2,4,5,7,9,12
	3,5,7,8,9,10,11,12,13,14
	0,1,2,3,6,10,13,15
	0,3,5,6,7,11,13,15
	0,1,2,4,5,8,11,14,15
	3,4,5,7,8,11,12,13,15
	1,2,3,4,9,10,11,14,15
	0,1,6,7,8,9,12,15
	0,1,3,5,9,10,12,13
	0,2,3,4,5,10,11,13,15
	0,1,2,3,4,7,8,12,14,15
	1,2,3,4,6,9,14,15
	1,2,5,6,7,11,12,15,
	0,3,6,8,10,11,13,14,15
	2,3,4,5,7,11,13,15

Примечание: Список вариантов заданий для трех студенческих групп приводится в таблицах. Порядковый номер фамилии студента в списке группы является номером варианта задания данного студента.

Теоретические сведения, рекомендации и пояснения к выполнению домашних заданий

Алгебра логики оперирует с переменными, которые могут принимать только два значения, условно обозначаемые как 0 и 1. Совокупность значений n переменных x_n,…, x₁ называется набором.

Функция f(x_n,…,x₁) n переменных называется функцией алгебры логики, если она, также как и ее переменные, может принимать только два значения – 0 или 1. ФАЛ называется также переключательной, булевой или логической функцией.

Способы задания ФАЛ

ФАЛ может быть задана словесно, алгебраическим выражением, таблицей ее значений, которая называется таблицей истинности, номерами наборов переменных, на которых она равна единице ( или нулю ) и другими способами. Табличное задание любой ФАЛ в зависимости от значений ее переменных возможно потому, что область ее определения конечна.

Любая ФАЛ n переменных определена на 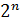наборах. Число различных ФАЛ n переменных конечно и равно .

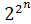Действительно, ФАЛ n переменных определена на 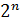наборах, на которых она может принимать значения 0 или 1. Поэтому в соответствие каждой ФАЛ можно поставить 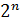-разрядное двоичное число. Так как количество различных 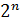-разрядных двоичных чисел равно 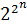_, то и количество различных ФАЛ равно .

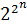Каждому набору переменных приписывают десятичный номер, эквивалентный двоичному числу, образованному совокупностью нулей и единиц данного набора. При этом переменные набора расположены в определенной последовательности, например, начиная с первого или наоборот.

Каждой ФАЛ приписывают десятичный номер, эквивалентный двоичному числу, образованному значениями функции, записанными слева направо, начиная со значения ФАЛ на нулевом наборе, т.е. на наборе переменных, содержащем все нули (0, 0, … , 0).

Например, функции f(x₃, x₂, x₁) и φ(x₃, x₂, x₁), заданные таблицей истинности (табл. 1), можно обозначить так: f(x₃, x₂, x₁)=f₈₄(x₃, x₂, x₁), φ(x₃, x₂, x₁)=f₄₅(x₃, x₂, x₁).

Таблица 1

№ набора	х3	х2	х1	f(х3, х2, х1)	φ(х3, х2, х1)

Набор переменных, содержащий все единицы (1, 1,…,1), называют также единичным набором.

Функцию f(x₃, x₂, x₁) можно также задать номерами 1, 3, 5 наборов переменных x₃, x₂, x₁ , на которых она равна единице (см. табл.1), функцию φ(х₃, х₂, х₁) –номерами наборов 2, 4, 5, 7.