Метод Рунге – Кутта 4-го порядка

Пусть дано дифференциальное уравнение первого порядка

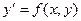
с начальным условием

y(x₀) = y₀.

Выберем шаг h и введём обозначения:

x_i = x₀ + i^.h и y_i = y(x_i) , ,

где i = 0, 1, 2, …

x_i – узлы сетки,

y_i- значение интегральной функции в узлах .

Аналогично описанным выше методам производится решение дифференциального уравнения. Отличие состоит в делении шага на 4 части.

Согласно методу Рунге – Кутта четвёртого порядка, последовательные значения y_i искомой функции y определяются по формуле:

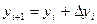
где

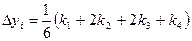, i = 0, 1, 2, …

а числа k₁⁽ⁱ⁾, k₂⁽ⁱ⁾, k₃⁽ⁱ⁾, k₄⁽ⁱ⁾ на каждом шаге вычисляются по формулам:

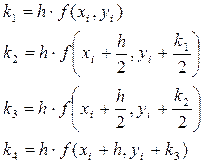
Это явный четырёхэтапный метод четвёртого порядка точности.

Методы Рунге – Кутта легко программируются и обладают значительной точностью и устойчивостью для широкого круга задач.

На рисунке 6 приведена блок-схема процедуры RUNGE(X0, XK, Y0, N, Y) для решения задачи Коши описанным выше методом Рунге – Кутта.

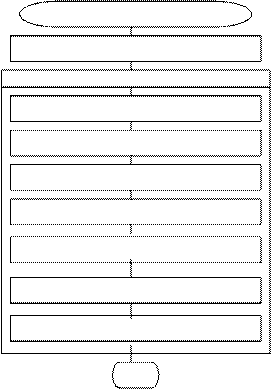RUNGE4 (X0,XK,Y0,N)

h=(XK – X0)/N

F(x, y) – заданная функция – должна быть описана отдельно. Входные параметры: X0, XK – начальное и конечное значения независимой переменной; Y0 – значение y0 из начального условия y(x0) = y0; N – количество отрезков разбиения; Выходные параметры: Y – массив значений искомого решения в узлах сетки;

i = 0, … , N-1

x = X0 + i * h

K1 = h * F(x, Yi)

K2 = h * F(x + h/2, Yi + K1 / 2)

K3 = h * F(x + h/2, Yi + K2 / 2)

K4 = h * F(x + h, Yi + K3)

K = (K1 + 2*K2 + 2*K3 + K4) / 6

Y_i+1 = Y_i + K

End

Рисунок 6 - Блок-схема процедуры RUNGE

На рисунке 7 приведена блок-схема алгоритма основной программы для решения задачи Коши и получения результатов с фиксированным количеством отрезков разбиения N. В основной программе происходит обращение к процедуре RUNGE(X0, XK, Y0, N, Y), вычисляющей значения искомой функции y_j в точках x_j методом Рунге – Кутта.

Исходными данными в данной задаче являются:

X0, XK – начальное и конечное значения независимой переменной;

Y0 – значение y₀ из начального условия y(x₀) = y₀;

N – количество отрезков разбиения.

Результаты работы программы выводятся в виде двух столбцов:

X – массив значений узлов сетки;

Y – массив значений искомого решения в соответствующих узлах сетки.

Ввод X0, XK, Y0, N

RUNGE(X0,XK,Y0,N,Y)

h=(XK-X0)/N

i=0…N

X=X0+i*h

Вывод X, Y_i

End

Рисунок 7 - Блок-схема алгоритма основной программы для решения задачи Коши с фиксированным количеством отрезков разбиения N

Решение дифференциальных уравнений в среде MathCad

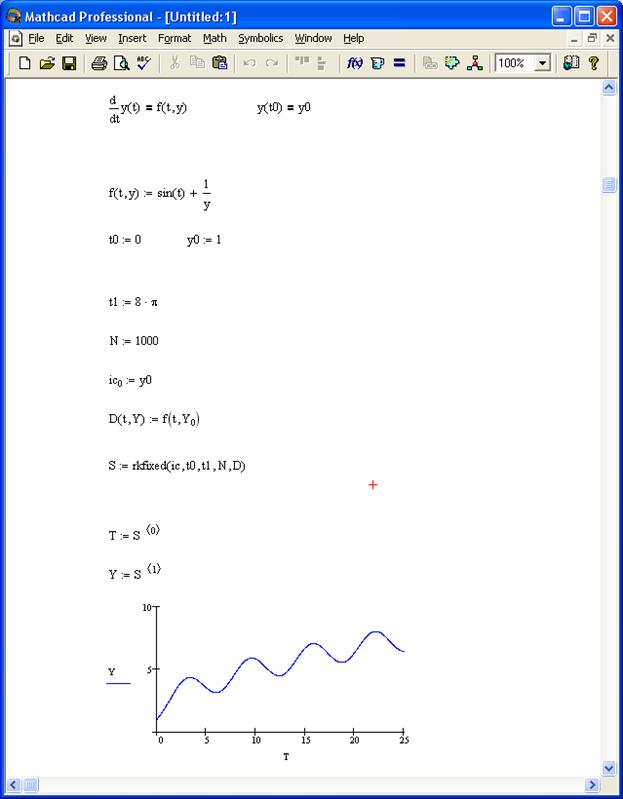
Рисунок 8 - Пример решения дифференциального уравнения методом

Рунге-Кутта 4 порядка в среде MathCad.

Построение графиков функций в среде Visual Basic

Задача табулирования функций и построения их графиков является одной из основных задач в процессе решения обыкновенных дифференциальных уравнений. Рассмотрим эту задачу более подробно.

Задача.

Построить график функции y=sin(x) на отрезке [a,b]. Шаг табулирования принять равным h.

Решение.

Для построения графика функции в среде Visual Basic удобно воспользоваться некоторыми графическими компонентами.

Рисунок 9 - Расположение основных компонентов в окне General

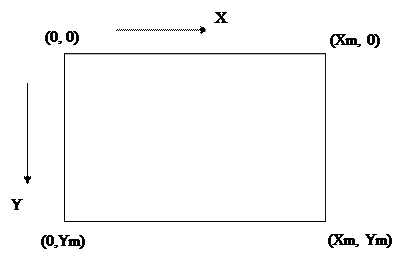
Компонент Picture Box ( ) используется в качестве контейнера для построения графика. Он представляет собой матрицу из точек (пикселей), причём имеется возможность управлять цветом каждой отдельной точки. Координаты любой точки определяются парой целых чисел – ее порядковым номером в строке Х и порядковым номером строки внутри объекта Y. Таким образом, координаты левого верхнего угла компонента (0, 0). Число точек в строке и число строк определяются размером компонента.

Рисунок 10 - Координаты объекта PictureBox

На рис. 10 показано расположение осей и координаты угловых точек объекта.

Компонент Line ( ) используется для построения осей и отрезков ломаной графика функции.

Суть построения графика сводится к тому, что функцию необходимо представить в виде таблицы (протабулировать), а затем отметить на шаблоне графика точки и соединить их между собой.

Алгоритм построения графика функции приведен на рисунке 12. Алгоритм может быть модифицирован. В частности, некоторые процедуры могут быть объединены, а порядок действий в некоторых случаях может быть изменен.

Рассмотрим алгоритм более подробно.

До реализации алгоритма необходимо описать подпрограмму- функцию для построения графика. Это необходимо для облегчения модификации программы. Если потребуется построение графика другой функции, достаточно будет только изменить подпрограмму.

Так же до построения графика необходимо создать и отредактировать форму. Пример разработки формы приведен на рисунке 11. На форме надо расположить компоненты для ввода исходных данных, компонент для вывода на печать таблицы, командную кнопку, контейнер для размещения графика (PictureBox). Внутри PictureBox надо нарисовать оси координат с помощью прямых линий и расположить метки для записи границ отрезка значений аргумента функции и экстремумов функции на рассматриваемом отрезке.

Ввод исходных данных осуществляется в рассматриваемой программе при нажатии на командную кнопку. Очень часто ввод данных реализуется с помощью компонента TextBox.

Процедуру табулирования функции удобно осуществлять в цикле с параметром, так как известно количество обсчитываемых точек графика. До выполнения процедуры надо задать количество строк таблицы.

Количество строк рассчитывается по формуле k=n+2, где k – количество строк, а n – количество отрезков табулирования. Число строк должно быть больше количества отрезков на 2, так как необходимо учесть начальную точку (нулевую) и строку для записи заголовков столбцов страницы.

В самой процедуре табулирования можно совместить два действия – табулирование и расчет экстремумов. Такой вариант решения приведен в листинге программы на рисунке13.

Основной сложностью построения графика является переход от математического значения функции и аргумента к экранным координатам, используемым для построения графика. При решении этой проблемы необходимо учитывать противоположное направление осей на математическом графике и на объекте PictureBox и необходимость масштабирования картинки.

Коэффициенты масштабирования графика рассчитываются по следующим формулам:

,

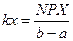где kx - коэффициент масштабирования по оси ОХ,

NPX – количество пикселей объекта PictureBox, отводимых для построения графика по горизонтали,

a – начальное значение отрезка аргумента функции,

b – конечное значение отрезка аргумента функции.

,

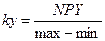где Ky - коэффициент масштабирования по оси ОY,

NPY – количество пикселей объекта PictureBox, отводимых для построения графика по вертикали,

min – минимальное значение функции,

max – максимальное значение функции.

Перевод математических координат текущей точки в экранные производится по формулам:

zx = Round(ox + (x(i) - a) * kx),

zy = Round(oy - (y(i) - Min) * ky),

где zx, zy – экранные координаты текущей точки,

ox, oy - координаты точки пересечения осей в компоненте pictureBox,

x(i), y(i) – математические координаты текущей точки,

kx, ky – коэффициенты масштабирования.

В формуле расчета экранной координаты ординаты текущей точки используется знак «минус» для учета противоположного направления осей (на экране и на графике).

Листинг программы построения графика функции приведен на рисунке 13.

Примеры форм с результатами работы программы для различных исходных данных приведены на рисунках 14 и 15.

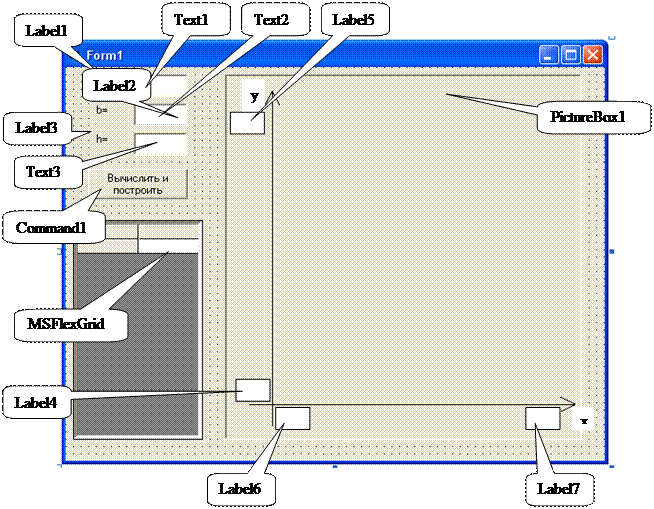
Рисунок 11 - Пример разработки формы

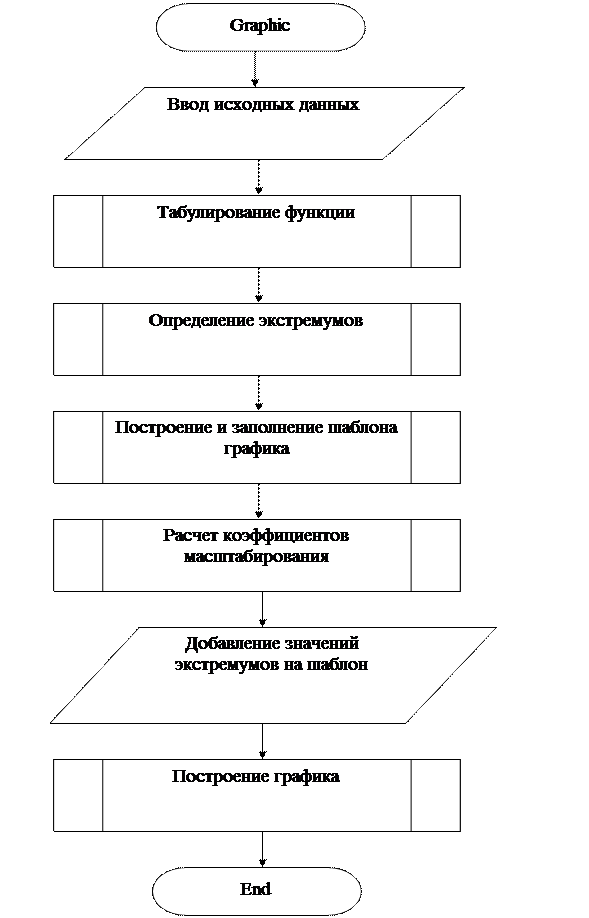
Рисунок 12 - Алгоритм построения графика функции