Последовательность решения. 1. Для построений задачи 9 необходимо найти натуральные величины образующих конуса
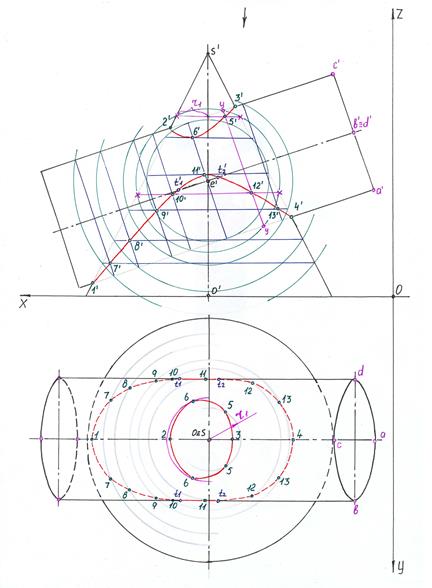
1. Для построений задачи 9 необходимо найти натуральные величины образующих конуса. Для этого из точки s (задача 8) проводим прямую, параллельную оси ОХ, и методом вращения разворачиваем все образующие конуса. Так как при развертывании основания конуса в окружность вписывают n-угольник, необходимо следить, чтобы угол между точками на окружности не превышал 30°, поэтому между точками а и а1 отмечаем точку х и между точками 101 и d отмечаем точку b1.
2. Последовательно поднимаем точки на ось ОХ, так как все точки находятся на основании конуса, и соединяем их с вершиной s'. Полученные образующие и есть натуральные величины.
3. Параллельно оси ОХ переносим на каждую образующую свои точки. Если образующих две, то на каждую переносим одноименные точки, например, образующие а's' и a1's' будут содержать точку 3.
4. Строим развертку конуса: проводим прямую произвольно на свободном месте поля чертежа, отмечаем на ней точку s. От нее откладываем по прямой натуральную величину образующей хs'. Так как на горизонтальную плоскость проекций основание конуса проецируется без искажения, то расстояние между образующими берем с основания конуса. Измеряем расстояние ха1 и откладываем на развертке от точки х, затем замеряем натуральную величину образующей s'a1 и из вершины s проводим дугу до пересечения с дугой ха1. Полученную точку пересечения дуг обозначаем а1. Полученную точку а1 соединяем с вершиной конуса s и откладываем на ней натуральную величину отрезка s'3. Так выстраиваем все точки, последовательно двигаясь по основанию конуса. Завершаем той же образующей, с какой начинали строить. Точки основания замыкаем плавной линией, точки линии пересечения также замыкаем между собой.
5. Строим развертку цилиндра. Боковая поверхность цилиндра представляет собой прямоугольник длиной, равной длине окружности основания цилиндра (2pR). Высота прямоугольника равна длине цилиндра, измеренной на горизонтальной плоскости проекций. Делим развертку на четыре равные части (т. к. у окружности всегда есть оси). Переносим точки на развертку основания цилиндра, измеряя расстояние между точками на фронтальной проекции основания цилиндра. Желательно, чтобы расстояние между точками также не превышало угол 30°; если угол больше, то для точности построения разбиваем дополнительными точками. Высоту расположения точек линии пересечения определяем на горизонтальной проекции цилиндра, измеряя расстояние от нижнего или верхнего основания цилиндра до точки (измерять необходимо перпендикулярно к основанию цилиндра). Полученные точки соединяем между собой.
Задача № 10
Методом сфер построить линию пересечения конуса и цилиндра. Данные к задаче представлены в таблице 7.
Указания к решению задачи № 10
По координатам строят поверхности конуса и цилиндра. Высота конуса для всех вариантов 100 мм, длина цилиндра – произвольная. Определяют точку пересечения осей конуса и цилиндра. Из точки пересечения осей как из центра проводят сферу произвольного радиуса. Сфера пересекает обе поверхности по окружностям, плоскости которых перпендикулярны осям поверхностей конуса и цилиндра. На пересечении этих окружностей, вырождающихся в прямые линии, находят общие точки для поверхностей конуса и цилиндра. Далее строят горизонтальную проекцию линии пересечения и определяют видимость поверхностей.
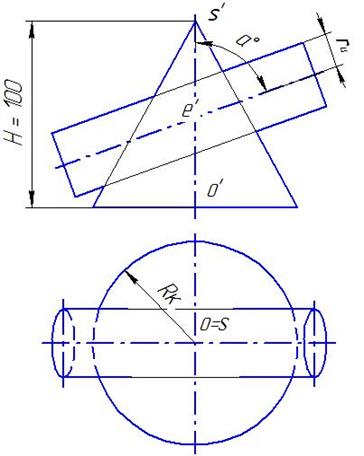
Таблица 7. Данные к задаче № 10
| Номер варианта | XО | YО | XЕ | ZЕ | RK | Rц | aО |