Нахождение параметров эмпирической зависимости методом наименьших квадратов

Пусть в результате эксперимента был получен ряд измерений величины 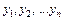, соответствующих значениям аргумента 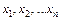, которые могут быть представлены на графике в виде точек 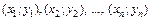(рис.1). Необходимо установить эмпирическую зависимость между переменными у и x. Следовательно, установить вид функции .

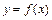Если соединить последовательно все эти точки, то получим ломаную линию, которая ничего общего не будет иметь с искомой зависимостью . Это следует хотя бы из того, что форма этой ломаной линии не будет воспроизводиться при повторных измерениях. Измеренные значения будут в общем случае смещены относительно искомой кривой как в сторону больших, так и в сторону меньших значений, вследствие статистического разброса (рис.2).

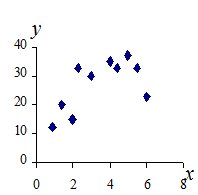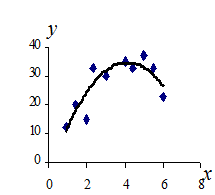Рисунок 1 – Поле экспериментальных данных	Рисунок 2 – Кривая 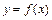, построенная по экспериментальным данным

Параметр, характеризующий результаты экспериментов, называют параметром оптимизации или функцией отклика.

Приближенную математическую модель процесса, найденную на основании экспериментальных данных, называют уравнением приближенной регрессии.

В общем виде задача ставится так: по данной выборке 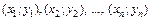построить уравнение регрессии и оценить допускаемую при этом ошибку.

Уравнение приближенной регрессии существенно зависит от выбираемого принципа приближенности. Подбирать это уравнение мы должны по значениям 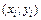. Поэтому здесь может возникнуть ошибка, связанная с тем, что самое точное уравнение для нескольких точек (а их у нас 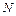) не гарантирует точности в промежуточных точках. Очевидно, бессмысленно пытаться строить такие уравнения, которые на всех парах чисел 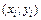давали бы точные равенства.

Соответствие математической модели процесса экспериментальным данным называют адекватностью. Уравнение адекватно описывает результаты опытов, если квадратичное отклонение значений параметров оптимизации, рассчитанных по уравнению регрессии, от экспериментальных данных обусловлено только ошибкой воспроизводимости.

Для определения параметров математической модели по результатам эксперимента будем применять один из методов регрессионного анализа – метод наименьших квадратов (МНК). К форме уравнения регрессии (зависимость типа 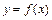) предъявляется требование линейности уравнения по параметрам или допущение возможности линеаризации. Например, процедура проведения регрессионного анализа одинакова для уравнени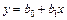й и 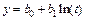, так как замена 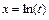превращает второе уравнение в первое. Специальные линеаризующие преобразования позволяют привести нелинейное по параметрам уравнение к линейному виду. Например, прологарифмировав уравнение 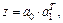получим 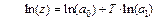. 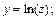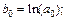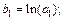После введения обозначений 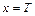получим уравнение 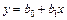. Определив коэффициенты 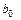и 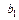, находят искомые параметры .

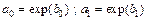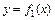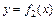Принцип наименьших квадратов вытекает из общего положения математической статистики, согласно которому в качестве меры рассеяния всегда берется дисперсия (среднее из суммы квадратов отклонений). Этот принцип позволяет сравнивать, какое из двух произвольных уравнений дает лучшее приближение регрессии. Пусть, например, заданы два уравнения: и . Согласно первому уравнению, значению 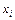должно соответствовать значение 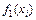. На самом же деле задано значение 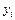, т. е. получается отклонение 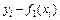. Общей мерой рассеяния всех 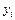вокруг функции 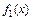будет величина

,

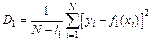где 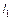— число связей, накладываемых на выборку данных функцией 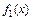. Аналогично получается мера рассеяния вокруг функции :

.

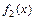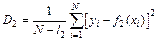Из функци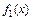й и 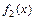мы должны теперь выбрать ту, у которой меньше соответствующая мера рассеяния 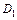или .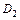

Принцип наименьших квадратов пригоден для сравнения любого числа функций. При этом удобнее всего сравнивать функции, накладывающие на выборку одинаковое число связей 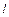, так как при этом можно сравнивать просто суммы квадратов отклонений (отсюда и название принципа). В общем виде этот принцип формулируется следующим образом.

Пусть задан некоторый класс функций 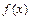, накладывающих на выборку одинаковое число связей. Тогда наилучшее уравнение приближенной регрессии дает та функция из рассматриваемого класса, для которой сумма квадратов отклонений между экспериментальными и рассчитанными по уравнению регрессии значениями выходного параметра имеет наименьшее значение.

.

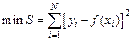В качестве класса сравниваемых функций берут обычно совокупность функций зафиксированного типа, но с произвольными коэффициентами, например, совокупность всех многочленов фиксированной степени 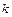. Чтобы выбрать среди всех этих функций лучшую, нужно найти ее коэффициенты. Эти коэффициенты вычисляются по экспериментальным данным и поэтому представляют собой некоторую связь, наложенную на выборку. Вследствие этого число связей 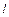, накладываемых функцией 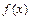на выборку, равно числу неопределенных коэффициентов, входящих в аналитическое выражение этой функции. Например, для многочленов степени 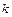число связей равно .

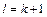Очень часто для описания экспериментальных данных удается ограничиться уравнением первой степени, которое накладывает на выборку лишь две связи.

Обычно уравнение приближенной регрессии находят по этапам: сначала определяют коэффициенты линейного уравнения, затем добавляют квадратный член и при необходимости члены более высоких порядков. При каждой новой добавке нужно проверять, чтобы не увеличилась дисперсия 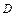(за счет увеличения числа связей 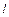), в противном случае от добавки нужно отказаться.