Что происходит с продольным и поперечными размерами стержня при растяжении (сжатии)? Связана ли поперечная деформация с продольной деформацией стержня?
Пусть в результате деформации первоначальная длина стержня l станет равной l1. Изменение длины
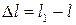
называется абсолютным удлинением стержня. Оно измеряется в единицах длины, например, в сантиметрах (см).
Отношение абсолютного удлинения стержня к его первоначальной длине называется относительным удлинением или продольной деформацией. Эта безразмерная величина обозначается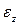 
(эпсилон) и вычисляется по формуле
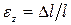. (2.3)
При растяжении продольная деформация считается положительной, а при сжатии – отрицательной.
Поперечные размеры стержня в результате деформирования также изменяются, при этом при растяжении они уменьшаются, а при сжатии – увеличиваются. Если материал является изотропным, то его поперечные деформации в направлении осей x и y равны между собой: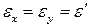 
.
Опытным путем установлено, что при растяжении (сжатии) в пределах упругих деформаций отношение поперечной деформации к продольной является постоянной для данного материала величиной. Абсолютная величина этого отношения
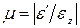
называется коэффициентом поперечной деформации или коэффициентом Пуассона – по имени французского ученого Симеона Дени Пуассона (Poisson, 1781 – 1840 гг.). Для различных материалов коэффициент Пуассона изменяется в следующих пределах: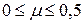 
. Например, для пробки 
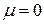, для каучука 
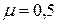, для стали 
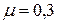, а для золота 
.
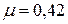2.8. Почему коэффициент Пуассона не может принимать значение большее, чем 0,5?
Для того чтобы ответить на этот вопрос, определим изменение объема стержня, имеющего, например, прямоугольное поперечное сечение с размерами b и h, при его растяжении.
Длина стержня l увеличится и станет равной
.
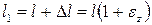Поперечные размеры b и h уменьшатся:
.
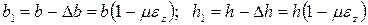Площадь поперечного сечения после деформации будет равна:
.
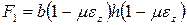Учитывая, что деформация 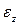мала и пренебрегая величиной 
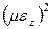по сравнению с единицей, получим:
.
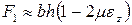Тогда объем стержня после деформации определится по формуле
.
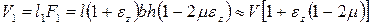Трудно себе представить, что при растяжении объем стержня уменьшится. Тогда из условия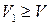 
найдем, что 
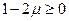. Или, окончательно,
.
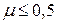2.9. Как записывается закон Гука при растяжении (сжатии)?
Для большинства материалов в пределах упругих деформаций между напряжением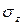 
и продольной деформацией 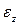существует линейная зависимость
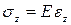. (2.4)
Напряжение пропорционально деформации – так формулируется в настоящее время закон Гука.
Впервые этот закон был опубликован в виде анаграммы ceiiinosssttuv в 1676 г. английским ученым Робертом Гуком в его работе «Десяток изобретений, которые я намерен опубликовать». При правильной расстановке букв анаграмма читается следующим образом: «Ut tensio, sic vis». В переводе с латинского языка это означает: «Каково удлинение, такова и сила».
Заметим, что к такому же заключению в 1680 г., независимо от Гука, пришел и французский ученыйЭдме Мариотт (Mariotte, 1620 – 1684 гг.).
Коэффициент пропорциональности E, стоящий в формуле (2.4), называется модулем продольной упругости или модулем Юнга – по имени английского ученого Томаса Юнга (Iounge, 1773 – 1829 гг.). Его значение для данного материала может быть установлено только опытным путем. В справочниках обычно приводится среднее значение модуля Юнга.
Иногда модуль Юнга называют и «модулем упругости первого рода». Однако использование этого термина в настоящее время не рекомендуется.
Заметим, что существуют материалы (например, чугун), которые лишь с некоторым приближением можно считать подчиняющимися закону Гука. А такие материалы, как кожа и ткани, и вовсе ему не подчиняются.
Необходимо также отметить, что материалы, которые подчиняются закону Гука, перестают ему следовать при достижении деформации (напряжения) определенного значения.
2.10. Что характеризует модуль продольной упругости? В каких единицах он измеряется?
Из формулы (2.4) видно, что чем больше модуль Юнга, тем меньше (при том же значении напряжения) деформация материала. Следовательно, модуль продольной упругости характеризуетжесткость материалапри растяжении (сжатии). Из этой же формулы видно, что модуль Юнга измеряется в тех же единицах, что и нормальное напряжение .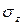
Так, например, для всех марок сталей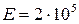 
МПа, для алюминиевых сплавов 
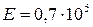МПа, для пленки скорлупы яйца 
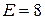МПа, а для алмаза 
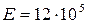МПа.
К сожалению, само название – модуль продольной упругости – провоцирует иногда студента на неверное истолкование его физического смысла. Так, на вопрос о том, что он характеризует, зачастую можно
услышать следующий неверный ответ: «Модуль Юнга характеризует
упругость материала. Поэтому, чем он больше, тем больше упругость
материала».
Напомним, что упругость – это способность восстанавливать первоначальные размеры и форму после снятия внешней нагрузки. Следовательно, к упругости, в этом смысле слова, модуль Юнга не имеет никакого отношения. Закон Гука, в котором фигурирует модуль продольной упругости E, говорит нам о том, что напряжение пропорционально деформации только в пределах упругих деформаций. И именно в том смысле следует понимать слово «упругость» в упомянутом термине.