Дизъюнктивная и коньюктивная нормальные формы

Билет №1

Логические функции. Таблица истинности.

В русском языке сложные предложения получаются путем соединения простых предложений с помощью союзов а, но, если .. то, тогда и только тогда, когда, или, и, аналогично в алгебре логики простые высказывания соединяются в сложные с помощью так называемых логических связок.

Если простое высказывание является истинным, то оно принимает значение логической переменной 1, иначе 0.

Основными операциями являются:

- Отрицание (не)

- Дизъюнкция (логическое сложение, v)

- Конъюнкция (логическое умножение,^)

- Импликация ( → )

- Эквиваленция (↔)

Отрицанием или инверсией высказывания А называется высказывание 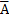, которое истинно, когда высказывание А ложно, и наоборот.

Дизъюнкцией высказываний А и В называется высказывание АvВ, которое истинно тогда и только тогда, когда истинно хотя бы одно из высказываний.

Конъюнкцией высказывания А и В называется высказывание А^В, которое истинно тогда и только тогда, когда истины оба высказывания.

Импликацией высказываний А и В является высказывание А→В, которое ложно тогда и только тогда, когда из истины следует ложь.

Эквиваленцией высказывания А и В называется высказывание А↔В, которое истинно тогда и только тогда, когда либо истинно либо ложно одновременно оба высказывания.

Соответствия в АЛ	Название операции	Талица истинности
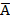	отрицание	А
АvВ	дизъюнкция	А В АvВ
А^В	конъюнкция	А В А^В
А→В	Импликация	А В А→В
А↔В	эквиваленция	А В А↔В

Билет №2

Дизъюнктивная и коньюктивная нормальные формы.

Литерой - называется элемент высказывания x или её отрицание.

Элементарной дизъюнкцией называется выражение следующего вида:

,

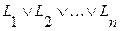где 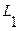- литера.

Элементарной конъюнкцией называется выражение следующего вида:

,

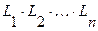Дизъюнктивной нормальной формой (ДНФ) формулы 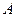называется выражение вида:

,

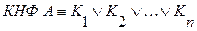где 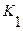- элементарная конъюнкция.

Конъюнктивной нормальной формой (КНФ) формулы 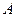называется выражение вида:

,

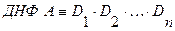где 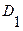- элементарная дизъюнкция.

Любую формулу можно представить в виде ДНФ или КНФ.

Совершеннойдизъюнктивной нормальной формой(СДНФ) формулы 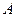называется такая ДНФ, для которой выполняются следующие условия:

1. Все элементарные конъюнкции, входящие в ДНФ 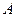, различны.

2. Все элементарные конъюнкции, входящие в ДНФ 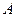, содержат литеры, соответствующие всем переменным.

3. Каждая элементарная конъюнкция, входящая в ДНФ 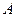, не содержит двух одинаковых литер.

4. Каждая элементарная конъюнкция, входящая в ДНФ 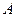, не содержит переменную и ее отрицание.

Совершеннойконъюнктивной нормальной формой(СКНФ) формулы 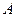называется такая КНФ, для которой выполняются следующие условия:

1. Все элементарные дизъюнкции, входящие в КНФ 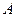, различны.

2. Все элементарные дизъюнкции, входящие в КНФ 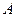, содержат литеры, соответствующие всем переменным.

3. Каждая элементарная дизъюнкция, входящая в КНФ 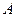, не содержит двух одинаковых литер.

4. Каждая элементарная дизъюнкция, входящая в КНФ 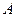, не содержит переменную и ее отрицание.

Билет №3