Таблицы с результатами измерений и вычислений.

Общие сведения

1. В этой работе изучаются вращательные колебания.

1. Маятник Обербека – насаженная на вал крестовина с передвигающимися по её стержням грузами, совершающая вращательные движения относительно вала под действием силы натяжения нити, намотанной на закреплённый на вал шкив.

Вращательное движение– такое движение твёрдого тела, при котором все его точки движутся по окружностям, центры которых лежат на одной прямой – оси вращения. Окружности, по которым движутся точки тела, лежат в плоскостях, перпендикулярных к этой оси.

Момент инерции тела – является мерой инертности тела при вращательном движении, подобно тому как масса тела является мерой инертности тела при поступательном движении.

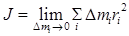или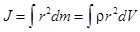

где Dm_i - масса элемента; r_i - расстояние от элемента до оси вращения; r - плотность вещества в элементе объема dV, находящегося на расстоянии r от оси вращения.

Инертность тел – свойство, присущее всем телам и заключающееся в том, что тела оказывают сопротивление изменению их скорости (как по модулю, так и по направлению).

Момент силы относительно точки – вектор, модуль которого равен произведению модуля силы на её плечо. Определяется как векторное произведение

,

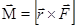где 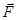- сила, 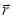- радиус-вектор, проведенный из данной точки, в точку приложения силы.

Момент силы относительно оси вращенияесть проекция 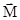на произвольную ось z, которая проходит через данную точку:

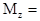
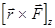
3. Основное уравнение динамики вращательного движения твердого тела

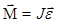
где М - суммарный момент внешних сил( 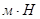), приложенных к телу относительно оси вращения; J - момент инерции тела ( 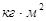) относительно той же оси; e - угловое ускорение ( ).

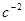Второй закон Ньютона: ускорение, с которым движется тело, прямо пропорционально силе, действующей на тело, совпадает с ней по направлению и обратно пропорционально массе тела.

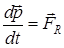- 2 закон Ньютона в импульсной форме

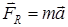, при m=const

1. В результате лабораторной работы ожидается получить график зависимости момента инерции от квадрата расстояния до оси вращения в виде прямо-пропорциональной зависимости, так как формула для расчета 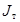имеет вид функции y=kx+b

Схема установки

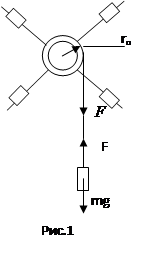mg - сила тяжести, H

F – сила натяжения нити, H

r_о - радиус шкива (м)

Расчетные формулы

1)

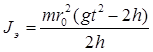
2)

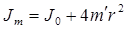
где m – масса груза (кг)

r_о - радиус шкива (м)

g - ускорение свободного падения (м/с²)

h - путь, пройденный грузом за время t (м)

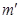- масса одного груза на крестовине (кг)

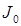- момент инерции грузов без крестовины (кг*м²)

r – расстояние от оси вращения до центра масс грузов (м)

Формулы погрешностей косвенных измерений

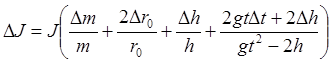
Погрешности прямых измерений:

1. Времени - 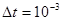(с)

2. Длины -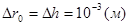

3. Массы -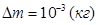

Таблицы с результатами измерений и вычислений.

Таблица 1

Физ. Величина	R	t		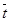Jэ	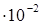Jр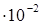
Ед.изм. № опыта	М	с	с	кг∙м2	кг∙м2
	0,25	12,314	12,114	4,68	11,03
11,987
12,021
	0,23	9,454	10,978	3,84	8,13
11,577
11,903
	0,21	10,286	10,350	3,41	8,09
10,265
10,500
	0,19	9,169	9,553	2,91	7,93
9,877
9,613
	0,17	8,868	8,743	2,43	7,56
8,690
8,671
	0,15	8,222	8,083	2,08	7,10
8,322
7,706
	0,13	7,126	7,150	1,63	6,89
7,524
6,801
	0,11	6,711	6,546	1,36	6,57
6,146
6,782
	0,09	5,763	5,826	1,08	6,32
5,710
5,007
	0,07	5,591	5,304	0,89	6,19
5,173
5,150

Таблица 2

Физ. Величина	ri	xi	Ji	x2i	xiJi
Ед.измер. Номер опыта	М	м2	кг∙м2	м4	кг∙м4
	0,25	0,0625	4,68	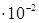3,9∙10-3	2,90∙10-3
	0,23	0,0529	3,84	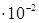2,8∙10-3	2,00∙10-3
	0,21	0,0441	3,41	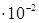1,9∙10-3	1,50∙10-3
	0,19	0,0361	2,91	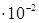1,3∙10-3	1,10∙10-3
	0,17	0,0289	2,43	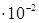0,8∙10-3	0,70∙10-3
	0,15	0,0225	2,08	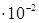0,5∙10-3	0,50∙10-3
	0,13	0,0169	1,63	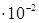0,3∙10-3	0,30∙10-3
	0,11	0,0121	1,36	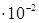0,1∙10-3	0,16∙10-3
	0,09	0,0081	1,08	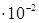0,06∙10-3	0,08∙10-3
	0,07	0,0049	0,89	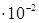0,02∙10-3	0,04∙10-3
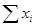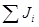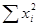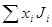		0,289	2,431	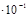0,116∙10-2	9,28∙10-2

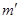=0,192 кг

h=0,43 м

r=0,023 м

m=0,053 кг